Bài 6. Friedman’s ANOVA (Friedman’s ANOVA)

Kiểm định Friedman là phương pháp thay thế phi tham số cho ANOVA một chiều với các phép đo lặp lại. Nó được sử dụng để kiểm tra sự khác biệt giữa các nhóm liên quan khi biến phụ thuộc được đo lường là thứ tự. Nó cũng có thể được sử dụng cho dữ liệu liên tục đã vi phạm các giả định cần thiết để chạy ANOVA một chiều với các biện pháp lặp lại (ví dụ: dữ liệu có sự sai lệch rõ rệt so với bình thường).

1. Khi nào sử dụng?

Kiểm định Friedman’s ANOVA theo các xếp hạng (ranks) cần được xem xét khi nhà nghiên cứu quan tâm đến việc kiểm tra sự khác biệt giữa các nhóm liên quan (các phép đo lặp lại) và khi các phép đo được xếp hạng tự nhiên hoặc có thể được xếp theo thứ tự. Bài kiểm tra có thể được coi là một phần mở rộng của bài kiểm tra hạng dấu Wilcoxon (Wilcoxon signed ranks test), với nhiều hơn hai điều kiện. Nó đặc biệt thích hợp cho các thiết kế thử nghiệm trong các đối tượng của tâm lý học và giáo dục. Thông thường, một biến phản hồi là một điểm đại diện, chẳng hạn như số mục đúng, số lỗi hoặc số nhiệm vụ đã hoàn thành.

Kiểm định này thực tế nhất khi có ít nhất năm đối tượng và tối thiểu bốn điều kiện (các phép đo lặp lại). Với ít các đối tượng hoặc các điều kiện hơn, nên tham khảo phân phối mẫu chính xác χ²_FR của thống kê thử nghiệm. Với hơn ba điều kiện và nhiều đối tượng hơn, χ²_FR gần đúng với phân phối χ². Kiểm định này dựa trên ý tưởng rằng theo giả thuyết vô hiệu không có sự khác biệt giữa các điều kiện (phép đo lặp lại), chúng ta mong đợi các giá trị xếp hạng được phân phối ngẫu nhiên trong mỗi điều kiện. Chúng ta cũng mong đợi tổng hạng (rank sum) và trung bình xếp hạng (mean rank) trong mỗi điều kiện là tương tự.

Việc thiết kế các phép đo lặp lại nhằm mục đích loại bỏ sự thay đổi nội bộ đối tượng (intra-subject variability) và do đó so sánh giữa các điều kiện nhạy cảm hơn với các hiệu ứng điều trị. Nếu tổng xếp hạng (rank sum) cho các điều kiện khác nhau là không bằng nhau, điều này cho thấy rằng điểm số trong mỗi điều kiện được lấy từ các dân số là khác nhau. Bài kiểm tra xếp hạng Friedman là đặc biệt nhạy cảm với sự khác biệt dân số trong xu hướng trung tâm (central tendency) và thường được coi là mạnh mẽ hơn bài kiểm tra Q Cochran (Cochran’s Q test).

2. Suy luận thống kê và giả thuyết vô hiệu

Giả thuyết vô hiệu được kiểm tra là các phép đo lặp lại (điều kiện) đã được lấy mẫu từ một quần thể duy nhất (hoặc k- quần thể có cùng các trung vị), giả thuyết thay thế là ít nhất một trong các điều kiện có giá trị trung vị khác với các điều kiện khác. Trong tình huống này, tổng xếp hạng (rank sum) và trung bình xếp hạng (mean rank) cho mỗi điều kiện sẽ khác nhau.

3. Giả định kiểm tra

Khi bạn chọn phân tích dữ liệu của mình bằng cách sử dụng bài kiểm tra Friedman’s ANOVA, một phần của quy trình bao gồm việc kiểm tra để đảm bảo rằng dữ liệu bạn muốn phân tích thực sự có thể được phân tích bằng bài kiểm tra Friedman’s ANOVA. Bạn cần phải làm điều này vì chỉ thích hợp sử dụng bài kiểm tra Friedman’s ANOVA nếu dữ liệu của bạn “vượt qua” các giả định bắt buộc đối với bài kiểm Friedman’s ANOVA để cung cấp cho bạn kết quả hợp lệ.

• Dữ liệu xem xét bao gồm ba mẫu liên quan trở lên.
• Dữ liệu mỗi nhóm là một mẫu ngẫu nhiên từ dân số.
• Biến phản hồi (biến phụ thuộc) được đo lường ít nhất ở mức thứ tự (ordinal level). Ví dụ về các biến số thứ tự bao gồm thang đo Likert (ví dụ: thang điểm 7 từ đồng ý đến rất không đồng ý), trong số các cách xếp hạng danh mục khác (ví dụ: thang đo 5 điểm giải thích mức độ thích của khách hàng đối với một sản phẩm, từ ” Không nhiều lắm “thành” Có, rất nhiều “). Ví dụ về các biến liên tục bao gồm thời gian ôn tập (đo bằng giờ), trí thông minh (đo bằng điểm IQ), thành tích thi (đo từ 0 đến 100).
• Biến phản hồi có phân phối liên tục cơ bản.
• Mẫu KHÔNG cần phải được phân phối bình thường.

4. Thủ tục kiểm tra Friedman’s ANOVA

Ví dụ, một nhà nghiên cứu muốn xem xét liệu âm nhạc có ảnh hưởng đến nỗ lực tri giác cần thiết để thực hiện một bài thể dục hay không. Biến phụ thuộc là “nỗ lực tri giác để thực hiện bài thể dục” và biến độc lập là “loại nhạc”, bao gồm ba nhóm: “không nhạc”, “nhạc cổ điển” và “nhạc sôi động”. Để kiểm tra xem âm nhạc có ảnh hưởng đến nỗ lực tri giác cần thiết để thực hiện một bài thể dục hay không, nhà nghiên cứu đã tuyển chọn 20 vận động viên, mỗi người chạy ba lần trên máy chạy bộ trong 30 phút. Để nhất quán, tốc độ máy chạy bộ là như nhau cho cả ba lần chạy. Theo thứ tự ngẫu nhiên, mỗi đối tượng chạy: (a) không nghe nhạc gì cả; (b) nghe nhạc cổ điển; và (c) nghe nhạc sôi động. Vào cuối mỗi lần chạy, các đối tượng được yêu cầu ghi lại mức độ khó của phiên chạy trên thang điểm từ 1 đến 10, với 1 là dễ và 10 là cực kỳ khó (thang mức độ liên tục).

Giả thuyết vô hiệu được kiểm tra là các loại nhạc khác nhau không ảnh hưởng đến mức độ nỗ lực tri giác cần thiết để thực hiện bài thể dục ‘chạy bộ’. Giả thuyết thay thế là ít nhất một cặp phép đo lặp lại (cặp loại nhạc) có xu hướng hướng tâm khác nhau (trung vị).

Các dữ liệu và một phần tính toán của một bài kiểm tra Friedman là được trình bày trong bảng dưới đây.

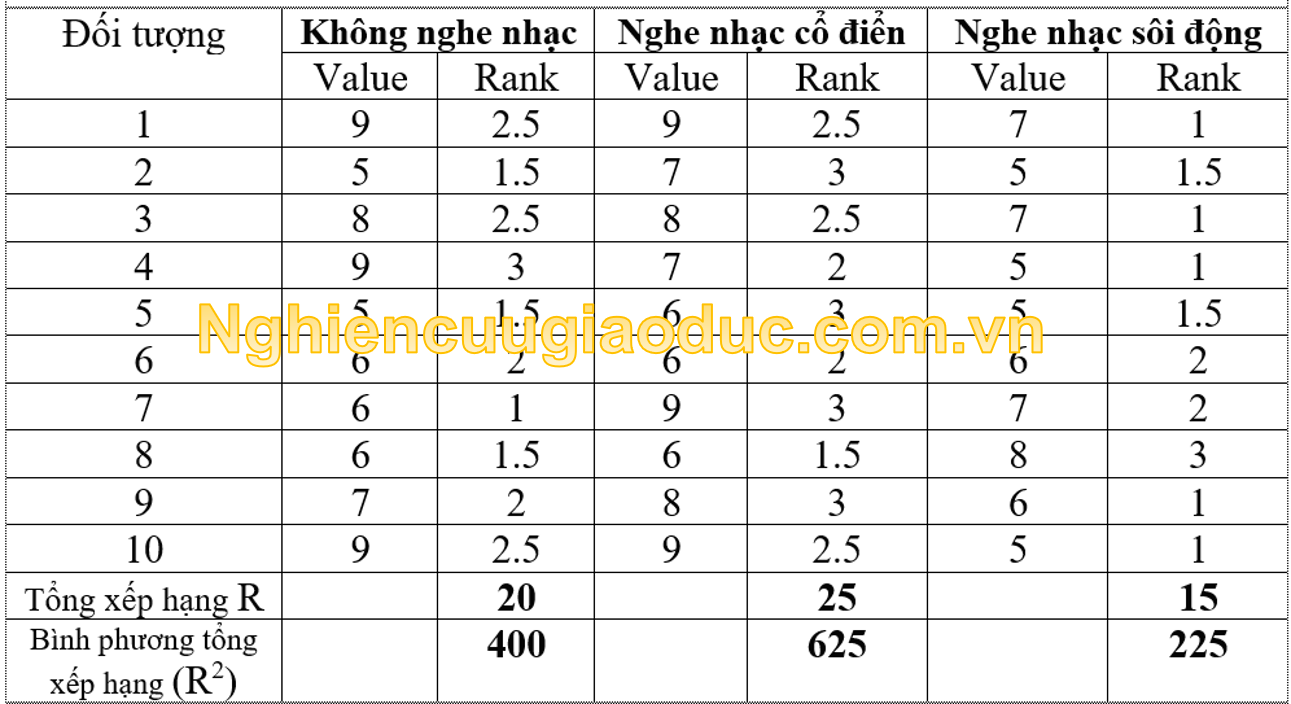
Trong bảng trên, khi xếp hạng giá trị dữ liệu, số điểm ít nhất cho cảm nhận mức độ khó của phiên chạy là nhận được xếp hạng 1 và điều kiện (loại nhạc) với số điểm cao nhất cho cảm nhận mức độ khó của phiên chạy là nhận được xếp hạng 3 (được xếp hạng trên ba điều kiện). Các số điểm bằng nhau được gán giá trị xếp hạng trung bình. Alpha được thiết lập 5%.

Các bước tính toán Friedman’s ANOVA:

Bước 1. Đối với mỗi đối tượng, biến phản hồi được xếp hạng theo ba điều kiện. Điểm nhỏ nhất được xếp hạng 1.

Bước 2. Tổng xếp hạng (R) và bình phương tổng xếp hạng (R²) cho mỗi điều kiện được đánh giá.

Bước 3. Sử dụng dữ liệu được trình bày trong bảng trên để tính thống kê kiểm tra Friedman, χ²_FR, theo công thức sau:

trong đó: N = số đối tượng (hoặc tập hợp các đối tượng trùng cặp – matched subjects);

• k = số điều kiện (các biện pháp lặp lại);
• R_j = tổng thứ hạng của các điều kiện (tức là tổng thứ hạng cho mỗi biện pháp lặp lại);
• g_i = số lượng các giá trị thứ hạng khác nhau cho đối tượng thứ i;
• t_ij = số lượng của các quan sát của giá trị xếp hạng thứ j trong đối tượng thứ i.

Ví dụ, hãy xem xét đối tượng đầu tiên trong bảng trên. Có 3 giá trị thứ hạng khác nhau, đó là g_i = 2, các giá trị thứ hạng này là 2.5 (2 quan sát), 1 (một quan sát), do đó:

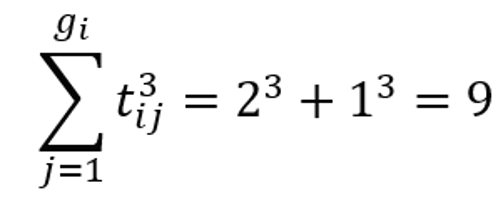
Nếu không có giá trị bằng nhau trong dữ liệu được xếp hạng thì:

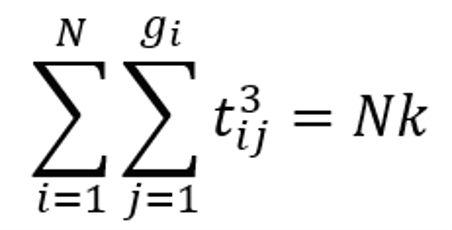
Tuy nhiên, điều đó không đúng trong ví dụ này. Dựa vào bảng trên, ta có:

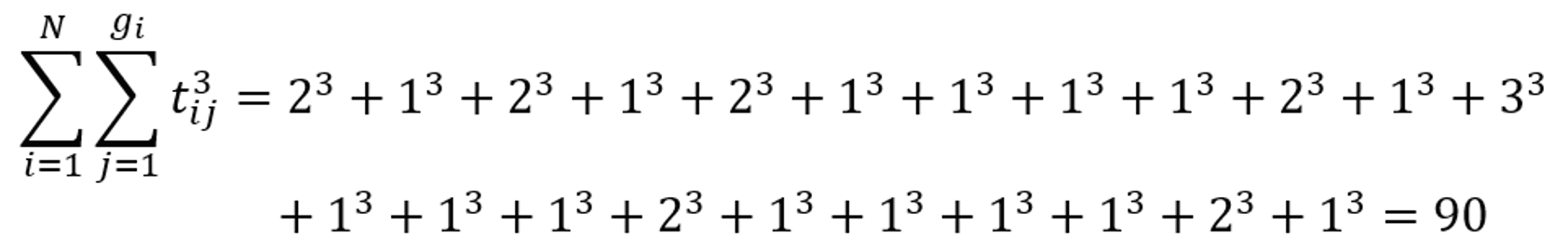
Tử số: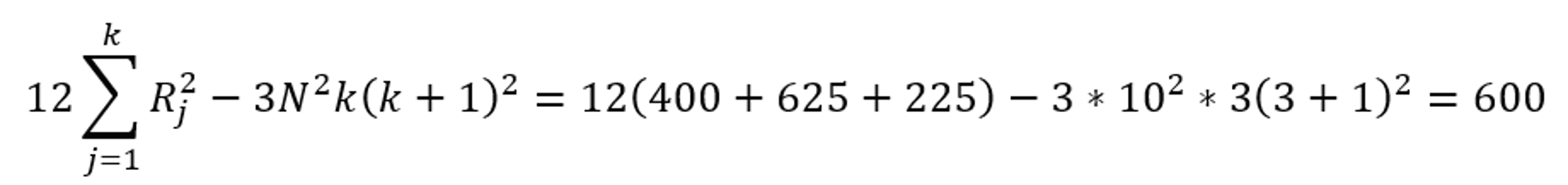

Mẫu số: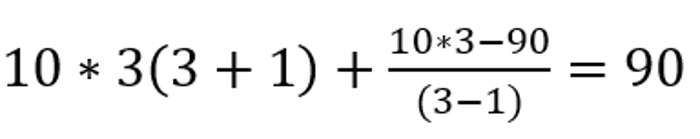 

Vậy: χ²_FR = 600/90=6.667

Kết quả này được đánh giá bằng cách sử dụng phân phối χ² với k − 1 bậc tự do để xác định giá trị tới hạn của χ² (vui lòng xem bảng phân phối χ²). Trong ví dụ này, χ² = 6.667 với 2 df và alpha được đặt thành 5% lớn hơn giá trị tới hạn (5.991).

Nhận xét: Giá trị χ² (6.667) quan sát là lớn hơn χ² tới hạn (5.991) nên giả thuyết vô hiệu bị bác bỏ, chúng ta có thể kết luận rằng trung bình xếp hạng (trung vị) cho 3 điều kiện là khác nhau đáng kể. Hay các loại nhạc có ảnh hưởng đáng kể đến tri giác về mức độ khó của phiên chạy.

Bước 4. Kiểm tra post hoc cho các so sánh đa cặp (Pairwise Multiple-Comparisons). Tương tự như kiểm tra Kruskal-Wallis, khi thống kê kiểm tra của Friedman’s ANOVA thu được là có ý nghĩa, nhà nghiên cứu cần xác định điều kiện nào (các phép đo lặp lại) khác nhau. Kết quả phân tích post hoc được tìm thấy trong kết quả của SPSS được thực hiện ngay sau đây.