Bài 1. Ý nghĩa của xác suất và suy luận thống kê
1. Giới thiệu
Trong nghiên cứu Tâm lí và Giáo dục (cũng như các ngành khoa học xã hội khác), nhà nghiên cứu biết chỉ có thể biết được một lượng nhỏ thông tin bằng các quan sát trực tiếp. Lượng thông tin đó hoàn toàn không đủ cho hoạt động phát hiện tri thức mới của nhà nghiên cứu. Để có thể phát hiện các tri thức mới, nhà nghiên cứu phải rút ra nhiều thông tin mới từ các thông tin đã có, tức là phải SUY LUẬN.
Hiểu đơn giản, suy luận là quá trình tâm lí mà một “kiến thức mới” được suy ra từ nhiều thông tin “quan sát được”. Hay nói khác đi, một ý niệm mới/ tư tưởng mới được suy ra từ các tri thức đã biết. Những ý niệm mới này được gọi là những giả thuyết (hoặc câu hỏi nghi vấn) cần được kiểm chứng khoa học dựa trên các số liệu thu thập từ quan sát, khảo sát, thực nghiệm, trải nghiệm. Trong các nghiên cứu định lượng về Tâm lý & Giáo dục, để kiểm chứng các suy luận khoa học, chắc chắn, nhà nghiên cứu cần phải sử dụng các phân tích thống kê (với công cụ SPSS, hoặc Lập trình R, AMOSS hoặc đơn giản là Excel).
Bản chất của phân tích thống kê (statistical anylysis) là nỗ lực tâm trí của nhà nghiên cứu để cố gắng chuyển từ các dữ liệu thực nghiệm/ khảo sát sang việc trả lời các câu hỏi nghiêu cứu (giả thuyết nghiên cứu) bằng việc giải thích ý nghĩa của xác suất (probability) và suy luận thống kê (statistical inference).
2. Tại sao “xác suất” phải được sử dụng trong quá trình nghiên cứu?
Một quá trình nghiên cứu định lượng thường bắt đầu với một câu hỏi nghiên cứu. Chẳng hạn, ‘liệu kết quả kỳ thi viết cuối kì môn Toán giải tích có thể được dự đoán dựa trên thời gian ôn tập của các sinh viên hay không?’, ‘liệu âm nhạc có ảnh hưởng đến nỗ lực tri giác cần thiết để thực hiện một bài thể dục chạy bộ hay không?’ Nếu một trường có khoảng 35.000 sinh viên, liệu chúng ta có cơ hội để điều tra/ thu thập thông tin từ tất cả người trả lời. Đó là khi chúng ta sử dụng đến ý nghĩa/ vai trò của xác suất trong quá trình nghiên cứu.
Ý nghĩa của thống kê về xác suất và suy luận thường ẩn mình vào trong mỗi bước của quá trình nghiên cứu định lượng (xem Hình 1).
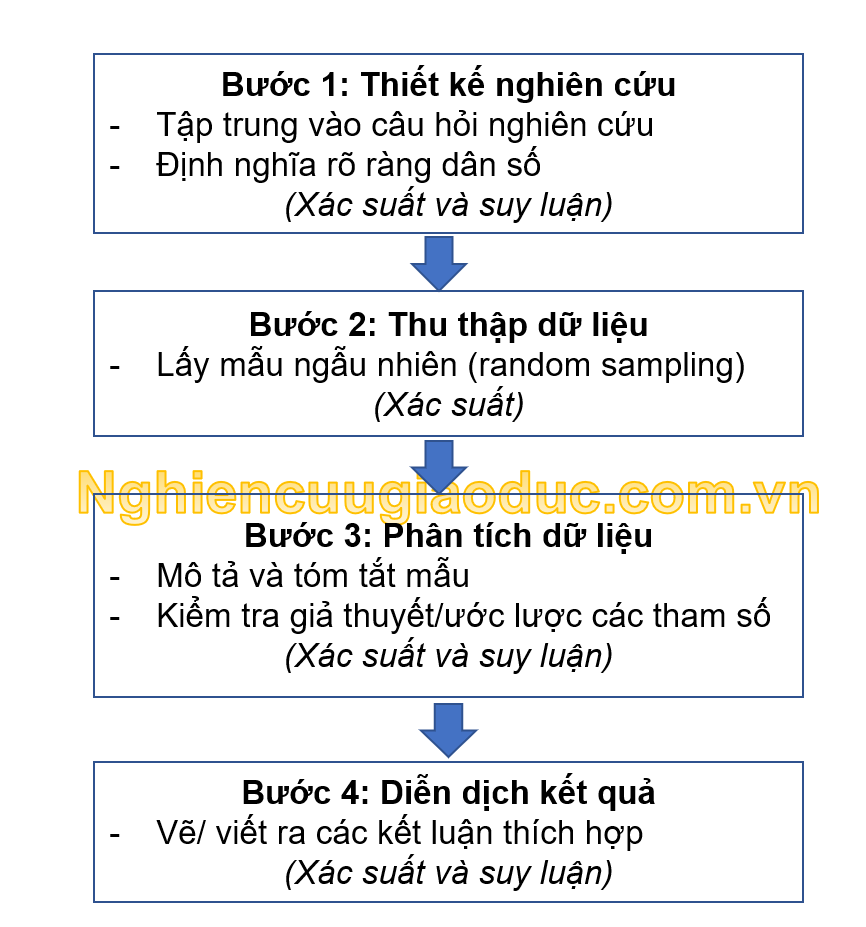
Hình 1. Quá trình nghiên cứu định lượng
Các câu hỏi nghiên cứu thường hàm ý rõ ràng đến các đối tượng quan tâm, chẳng hạn như tất cả giáo viên, tất cả sinh viên. Tuy nhiên, sau khi đã chỉ định một tập hợp dân số cụ thể (Bước 1), chúng ta thường không thể thu thập dữ liệu cho toàn bộ tập hợp dân số quan tâm. Thay vào đó, một “mẫu ngẫu nhiên” từ dân số được chọn để tiến hành các phân tích tiếp theo (Bước 2). Do đó, ngay trong Bước 1, chúng ta nên suy nghĩ cẩn thận về loại suy luận thống kê có thể có để trả lời các câu hỏi nghiên cứu trước khi thu thập dữ liệu.
Trong Bước 3, công việc đầu tiên trong phân tích dữ liệu tổng thể là việc mô tả và tóm tắt mẫu. Bằng việc sử dụng kỹ thuật đồ họa phân phối dữ liệu và thống kê tóm tắt để mô tả dữ liệu mẫu, chúng ta có thể xác định được các mô hình thống kê có thể có (Bước 3). Giai đoạn phân tích tiếp theo sẽ là các thủ tục chính thức với các bài kiểm tra thống kê cụ thể. Cuối cùng là những diễn dịch kết quả được rút ra (Bước 4).
3. Nguyên tắc nền tảng của suy luận thống kê
Chúng ta sử dụng suy luận thống kê (statistical inference) là khi chúng ta muốn vượt ra ngoài những phát hiện mô tả thu được từ dữ liệu mẫu để suy ra những điều gì đó sẽ xảy ra trong quần thể mẹ. Có hai khía cạnh để suy luận thống kê, bao gồm: ước lượng (estimation) và kiểm tra giả thuyết (hypothesis testing).
Ước lượng là để trả lời câu hỏi, “Giá trị của một tham số dân số (population parameter) là gì?”. Ví dụ, điểm trung bình của thành tích toán học của học sinh trung học là bao nhiêu?
Kiểm tra giả thuyết là để trả lời câu hỏi, “Xác suất hoặc khả năng xảy ra mà các tham số dân số bằng một giá trị xác định cụ thể là bao nhiêu?” Ví dụ, xác suất để điểm trung bình của thành tích toán học bằng 10 điểm là bao nhiêu? Từ đó, các bài kiểm định ý nghĩa thống kê được thực hiện để chỉ ra các bằng chứng chống lại các ‘giả thuyết thống kê’ đặt ra (Bước 3). Cuối cùng, các câu hỏi nghiên cứu được trả lời không chỉ dựa vào phát hiện từ một giả thuyết thống kê (statistical hypothesis), mà là sự tổng quát hóa những phát hiện này để suy luận đến một kiến thức mới vượt ra ngoài bối cảnh khảo sát hoặc thử nghiệm (Bước 4).
Tóm lại, các suy luận thống kê đóng vai trò trung tâm trong nghiên cứu định lượng. Tuy nhiên, giá trị cốt lõi của các suy luận thống kê (bao gồm: ước lượng và kiểm tra giả thuyết) không phải là đưa đến một kết luận khoa học, mà nó chỉ đơn giản là một sự trợ giúp cho việc “ra quyết định” của nhà nghiên cứu trong những trường hợp không chắc chắn. Nhờ có các thông tin tính toán của phân tích thống kê trong ước lượng và kiểm tra giả thuyết, một nhà nghiên cứu có thể đưa ra kết luận khoa học dựa trên (các) kết quả của (các) kiểm định thống kê.
4. Vai trò của xác suất trong chọn mẫu
Trong nghiên cứu định lượng, chúng ta có rất ít cơ hội thu thập dữ liệu cho toàn bộ dân số quan tâm. Bất cứ khi nào một mẫu được chọn từ toàn bộ dân số, một yếu tố không chắc chắn sẽ được đưa vào trong quá trình nghiên cứu. Sự không chắc chắn này là hệ quả của việc chúng ta không thu thập thông tin từ toàn bộ dân số, mà thay vào đó chỉ dựa vào thông tin có trong một mẫu nhỏ. Mức độ không chắc chắn này được biểu thị bằng “số học” dưới dạng xác suất đại diện khả năng xảy ra sự kiện.

Xác suất nói chung có thể được coi là nghiên cứu các mô hình của các sự kiện may rủi và dựa trên ý tưởng rằng những hiện tượng nhất định là ngẫu nhiên. Thống kê được tính toán từ dữ liệu mẫu và có thể được sử dụng không chỉ để tóm tắt dữ liệu mà còn để đánh giá mức độ mạnh mẽ của bằng chứng được cung cấp bởi dữ liệu mẫu ủng hộ một khẳng định hoặc tuyên bố trong toàn bộ dân số. Do vậy, các dữ liệu được cung cấp cần phải được tạo ra bởi một quy trình ngẫu nhiên (Bước 2), sau đó bản thân các thống kê mẫu, chẳng hạn như trung bình hoặc hệ số tương quan thuận/nghịch, có thể được coi là các biến ngẫu nhiên tuân theo quy luật xác suất. Do đó, chúng ta có thể sử dụng các ngôn ngữ của xác suất để đưa ra các tuyên bố về khả năng xảy ra các kết quả như sự khác biệt giữa các giá trị trung bình giữa hai biến số.
Một mẫu được tạo ra bởi một quá trình ngẫu nhiên được gọi là “mẫu xác suất” (probability sample) và các đối tượng hoặc giá trị mẫu sẽ được rút ra độc lập từ dân số. Điều này có nghĩa là cơ hội mà một đối tượng đã được lấy mẫu không phụ thuộc vào cơ hội mà các thành viên khác của dân số đã hoặc sẽ được lấy mẫu.
Một vấn đề lớn với nhiều thiết kế nghiên cứu định lượng là các mẫu phi xác suất là được xuất hiện. Một mẫu phi xác suất (non-probability) có thể phát sinh khi:
- Chúng ta không có danh sách mẫu, về cơ bản là danh sách mọi đối tượng trong dân số quan tâm;
- Không phải mọi thành viên của dân số đều có cơ hội được chọn độc lập;
- Không có mô hình xác suất cơ bản nào được chỉ định cho việc lấy mẫu. Điều đó có nghĩa rằng các thành viên của dân số không có cơ hội được chọn như nhau.
Hậu quả, các mẫu phi xác suất thường không đại diện cho dân số quan tâm và do đó, không nên dùng để suy luận thống kê. Ví dụ, trong những nghiên cứu thử nghiệm ‘trước’ và ‘sau’, việc giáo viên chủ nhiệm đề cử học sinh tham gia có thể là một mẫu phi xác suất. Hoặc, một giáo viên có thể không chọn một số học sinh tham gia vào một nghiên cứu thử nghiệm bởi những lý do khác, chẳng hạn, một đứa trẻ nói nhiều, phiền toái. Trong tất cả những trường hợp này, mẫu nghiên cứu là không đại diện cho toàn bộ dân số quan tâm, không xác định rõ dân số quan tâm là ai, nên nó không thể là mẫu xác suất.
Vì vậy, nếu trong một bài báo bạn đọc đã không xác định rõ một mẫu xác suất đại diện cho một dân số quan tâm, bạn không nên bị thuyết phục bởi (các) bằng chứng do tác giả cung cấp, các bài kiểm tra thống kê sẽ không có giá trị, và có thể các kết luận cũng không có giá trị. Bạn nên loại bỏ các nghiên cứu này ra khỏi tài liệu tham khảo của bạn hoặc bạn có thể phản biện lại chúng bởi những bằng chứng do bạn thực hiện.
5. Sự liên kết giữa xác suất và suy luận thống kê
Mối liên kết chính giữa xác suất và suy luận thống kê là sự phân phối mẫu (sampling distribution) của mẫu thống kê. Phân phối mẫu là phân phối các giá trị của thống kê khi các mẫu ngẫu nhiên độc lập riêng biệt có kích thước bằng nhau được lấy từ cùng một dân số. Phân phối mẫu là phân phối xác suất mô tả các giá trị có thể xảy ra của thống kê mẫu trong sự lặp lại mẫu, miễn là dữ liệu được tạo ra bởi một quá trình ngẫu nhiên. Đó là lí do giải thích cho tầm quan trọng của việc lấy mẫu ngẫu nhiên khi thu thập dữ liệu.
6. Ước lượng và kiểm tra giả thuyết
Trong Hình 1, sau khi đã xác định một dân số quan tâm và các câu hỏi nghiên cứu về các biến số cần đo lường, nhà nghiên cứu sau đó chọn một mẫu nên là mẫu xác suất ngẫu nhiên (Bước 2). Trong một mẫu ngẫu nhiên được chọn có thể xuất hiện sự biến thiên lấy mẫu (Sampling variability), được gọi tên là sai số mẫu (sampling error) trong các thiết kế khảo sát.
Khi nhà nghiên cứu chọn được một mẫu ngẫu nhiên, tính toán một giá trị thống kê, chẳng hạn như giá trị trung bình và sau đó vượt ra ngoài chức năng mô tả của thống kê nhằm sử dụng nó để xác định trung bình dân số, điều này được gọi là ước lượng (Estimation). Nói một cách đơn giản, ước lượng là khi chúng ta sử dụng “thống kê mẫu” để ước lượng giá trị của các tham số dân số. Các công thức được sử dụng để ước lượng thống kê được gọi là công cụ ước lượng.
Ví dụ, để giải quyết câu hỏi nghiên cứu về mối quan hệ giữa các kết quả học tập ở môn Toán và môn Khoa học của học sinh trung học, chúng ta có thể sử dụng thống kê mẫu “tương quan Pearson” (Pearson correlation), giá trị ‘r’ (thước đo mối quan hệ giữa hai biến), để ước lượng tương quan dân số ‘ρ’ (rho). Bất kỳ một mẫu nào được chọn ngẫu nhiên rất khó có khả năng giống với một mẫu ngẫu nhiên độc lập khác được chọn từ cùng dân số. Ví dụ, nếu các mối tương quan được tính toán cho hai mẫu độc lập thì không chắc chúng sẽ giống nhau. Điều này là do ‘sai số mẫu’ (sampling error). Sai số mẫu cũng cần được ước lượng để chúng ta có thể biết một thống kê ‘r’ tốt như thế nào đối với bất kỳ mối tương quan mẫu nào.
Do vậy, thay vì sử dụng thống kê ‘r’ để cố gắng ước tính một giá trị cụ thể của mối tương quan dân số, chúng ta có thể sử dụng nó để kiểm tra giả thuyết, ví dụ: ‘Mối tương quan dân số giữa kết quả học tập ở môn Toán và môn Khoa học của học sinh trung học có bằng 0 không?’ Ở đây, ý tưởng của xác xuất đã được sử dụng để hiểu liệu có hợp lý để tin rằng tham số dân số bằng 0 hay không. Trong thực tế, tham số dân số có thể là một giá trị thực khác 0 nhưng chúng ta không biết điều này. Logic của việc kiểm định giả thuyết đòi hỏi chúng ta giả định rằng mối tương quan dân số bằng 0 và chúng ta tích lũy bằng chứng để bác bỏ phỏng đoán này. Như vậy, việc sử dụng “kiểm tra giả thuyết” sẽ mang lại ý nghĩa cho phân tích thống kê hơn.
7. Diễn dịch các phân tích thống kê
Giai đoạn cuối cùng của quá trình nghiên cứu là diễn dịch các bài kiểm tra thống kê và đưa ra kết luận về quần thể mẹ dựa trên dữ liệu mẫu (Bước 4).
Việc diễn dịch cần được thực hiện thận trọng liên quan đến các sự hạn chế của thiết kế nghiên cứu, chẳng hạn, chúng ta có tin chắc rằng tính ngẫu nhiên đã đạt được trong thiết kế không? ví dụ, chỉ một số nhóm học sinh nhất định tham gia vào một nghiên cứu? Một thử nghiệm có thực tế không, ví dụ, một giải pháp sư phạm dựa trên việc đóng vai, liệu đây có phải là điều mà trẻ em lớp 5 và lớp 6 tuổi rất thường làm không? Chúng ta cũng nên liên hệ kết quả của mình với những phát hiện từ các nghiên cứu tương tự.
Công việc tiếp theo là việc lựa chọn các bài kiểm tra thống kê liên quan đến các câu hỏi nghiên cứu. Làm thế nào để chúng ta có thể bác bỏ một giả thuyết? Cơ hội phát hiện ra một mối quan hệ hoặc sự khác biệt nào nếu một mối quan hệ thực sự tồn tại? Cơ hội phát hiện ra sự khác biệt không thực sự tồn tại là gì? Mẫu của chúng ta phải lớn như thế nào? Sự biến thiên mẫu (sai số mẫu) có quan trọng không? Ước lượng của tôi chính xác đến mức nào và tôi nên có niềm tin vào nó không? Tôi nên sử dụng bài kiểm tra thống kê nào và tại sao? Để trả lời các câu hỏi này, xin vui lòng đọc bài “lựa chọn bài kiểm tra thống kê“.
Tài liệu tham khảo
- Coolican, H. (2018). Research methods and statistics in psychology. Routledge.
- Hanneman, R. A., Kposowa, A. J., & Riddle, M. D. (2012). Basic statistics for social research (Vol. 38). John Wiley & Sons.
- Jackson, S. L. (2015). Research methods and statistics: A critical thinking approach. Cengage Learning.
- McQueen, R. A., & Knussen, C. (2006). Introduction to research methods and statistics in psychology. Pearson education.
- Peers, I. (2006). Statistical analysis for education and psychology researchers: Tools for researchers in education and psychology. Routledge.
- Wagner III, W. E. (2019). Using IBM® SPSS® statistics for research methods and social science statistics. Sage Publications.




















