Bài 2. One-sample Runs Test về tính ngẫu nhiên (One-sample Runs Test for Randomness)

Nếu nhà nghiên cứu muốn kết luận về dân số bằng cách sử dụng thông tin có sẵn trong mẫu từ dân số đó, thì mẫu đó phải là ngẫu nhiên (random). Vì vậy các quan sát tiếp theo phải độc lập. Một số kỹ thuật đã được phát triển để kiểm tra giả thuyết rằng mẫu là ngẫu nhiên. Các kỹ thuật One-sample Runs Test này dựa trên thứ tự hoặc trình tự thu được các điểm số hoặc quan sát riêng lẻ.

1. Khi nào sử dụng?

Kiểm tra này được sử dụng bất cứ khi nào chúng ta muốn kết luận rằng một chuỗi của các sự kiện nhị phân là ngẫu nhiên. Suy luận cơ bản của thử nghiệm này là thứ tự (trình tự) của các quan sát thu được dựa trên mẫu là ngẫu nhiên. Nhiều thủ tục thống kê dựa trên giả định là mẫu ngẫu nhiên. Thử nghiệm chạy (runs test) cho phép kiểm tra giả định này nếu nghi ngờ tính ngẫu nhiên của mẫu. Thử nghiệm có thể được sử dụng như một phần của phân tích dữ liệu ban đầu.

Ví dụ, trong phân tích hồi quy, thường cần phải kiểm tra sự phân phối của các phần dư (sự khác biệt giữa giá trị quan sát của biến phản hồi và giá trị vừa vặn của mô hình hồi quy). Phần dư là dương hoặc âm và các dấu hiệu của phần dư được sắp xếp theo thứ tự xuất hiện của chúng. Một lần RUN là một chuỗi các sự kiện giống hệt nhau (+ hoặc -) được đặt trước hoặc theo sau bởi một sự kiện khác hoặc không có sự kiện nào cả (đầu và cuối một chuỗi). Sự thiếu ngẫu nhiên trong mẫu của phần dư được thể hiện bởi quá ít hoặc quá nhiều lần chạy và điều này cho thấy rằng một hoặc nhiều giả định cơ bản của phân tích hồi quy đã bị vi phạm. Thử nghiệm chạy sử dụng thông tin về thứ tự của các sự kiện không giống như các quy trình thử nghiệm danh nghĩa, chẳng hạn như thử nghiệm Chi-square sử dụng thông tin về tần suất của các sự kiện.

Ví dụ, một chuỗi sự kiện tuyến tính (được biểu thị bằng các ký hiệu cộng + và trừ -) xảy ra theo thứ tự sau:

– Điểm mẫu này bắt đầu với lượt chạy +2, tiếp theo là lượt chạy -3, chạy +1, chạy – =4, v.v. Chúng ta có thể nhóm các điểm số thành các lần chạy bằng cách gán một số cho mỗi dãy ký hiệu chỉ định. Vì vậy, chúng ta có bảy lần chạy hoặc U là số lần chạy = 7. Tổng số lần chạy trong một mẫu cho biết liệu mẫu đó có phải là ngẫu nhiên (random) hay không. Ví dụ, nếu một đồng xu được tung 20 lần, chuỗi đầu (H) và đuôi (T) sẽ xảy ra, được quan sát như sau:

HHHHHHHHHHTTTTTTTTTT

Trong trường hợp này, chỉ có hai lần chạy trong 20 lần tung đồng xu. Có vẻ như chỉ hai lần chạy là quá ít cho một lần ném “công bằng” và kết quả là không có sự độc lập của các sự kiện. Ngược lại, nếu tung 20 lần đồng xu sẽ tạo ra các sự kiện sau:

HTHTHTHTHTHTHTHTHTHT

Trong trường hợp này có rất nhiều lần chạy, cụ thể là U = 20, khi N = 20. Có vẻ như trong trường hợp này có xu hướng bác bỏ giả thuyết rằng việc tung đồng xu là “ngẫu nhiên”, bởi vì việc quan sát các sự kiện không dường như độc lập tức là có sự xuất hiện mối quan hệ hệ thống của H theo sau T theo thứ tự.

Gọi n₁ là số phần tử của một ký hiệu và n₂ là số phần tử của ký hiệu kia trong chuỗi sự kiện N = n₁ + n₂ của các lần xuất hiện nhị phân. Ở đây nó có thể n₁ là sự kiện đầu (H) và n₂ ở dạng sự kiện đuôi (T) khi tung đồng xu, hoặc nó có thể là n1 số dấu cộng (+) và n2 số dấu trừ (-) trong câu trả lời câu hỏi. Để sử dụng phương pháp chạy thử trên mẫu, đầu tiên là quan sát các sự kiện n₁ và n₂ và xác định số lần chạy (U). Nếu cả n₁ và n₂ đều nhỏ hơn hoặc bằng 20 thì sử dụng bảng dưới đây để cung cấp giá trị tới hạn cho U với H₀ và alpha có nghĩa = 0,05. Nếu số lượng U nằm giữa các giá trị tới hạn, thì chúng ta không thể bác bỏ H₀, nhưng nếu giá trị U được tính bằng hoặc lớn hơn giá trị tới hạn, thì chúng ta có thể bác bỏ H₀.

Ví dụ, trong trường hợp tung đồng xu đầu tiên ở trên, chúng ta nhận được 2 lần chạy, một lần chạy với 10 đầu, tiếp theo là một lần chạy với 10 mặt. Ở đây n₁ = 10, n₂ = 10, U = 2. Với các giá trị của n₁ = 10 và n₂ = 10, thực hiện tra bảng U tới hạn (vui lòng xem bảng U tới hạn tại đây), chúng ta sẽ ngẫu nhiên khi U trong khoảng 7 lần chạy đến 15 lần chạy với khoảng tin cậy 95%. Mỗi số lượng U bằng 6 trở xuống, hoặc 16 trở lên, nằm trong vùng từ chối với alpha = 0,05. Trong trường hợp với U = 2 trên giá trị của U nhỏ hơn 6, thì chúng ta có thể bác bỏ H₀.

Khi n₁> 20 (hoặc/và n₂> 20), có thể sử dụng phép xấp xỉ mẫu lớn. Nhà nghiên cứu chọn một thử nghiệm hai mẫu (two-sample test) và alpha = 0.05. Giả thuyết vô hiệu được kiểm tra bằng cách sử dụng xấp xỉ chuẩn cho phân phối mẫu của U. Khi n₁ hoặc n₂≥20, xác suất liên quan đến U quan sát được đánh giá bằng công thức dưới đây cho độ lệch Z chuẩn:

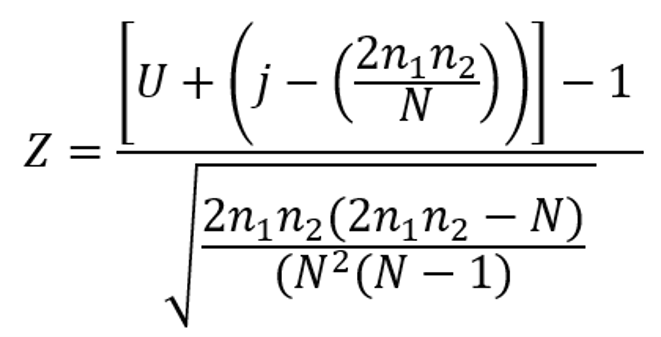
trong đó N là tổng kích thước mẫu, U là số lần chạy, n₁ và n₂ là tần số cho hai loại của biến đáp ứng và j là điều chỉnh cho tính liên tục trong đó nó là 0.5 nếu U <2n₁n₂ / (N + 1) hoặc −0,5 nếu U> 2n₁n₂ / (N + 1).

Nếu giá trị Z không lớn hơn giá trị tới hạn hai phía, +/− 1.96 (ở mức ý nghĩa alpha = 0.05), giả thuyết vô hiệu về tính ngẫu nhiên ở mức 5% được chấp nhận. Vì phân phối chuẩn là đối xứng, giá trị Z âm (-) có cùng xác suất liên quan với giá trị Z là dương (+). Từ bảng phân phối Z (vui lòng xem bảng phân phối Z) cho biết tỷ lệ của tổng diện tích dưới đường cong chuẩn vượt quá điểm + ve Z, giá trị p liên quan cho một Z là ý nghĩa nếu lớn hơn 0.05 (lưu ý rằng p-value được nhân đôi đối với thử nghiệm hai phía).

2. Suy luận thống kê và giả thuyết vô hiệu

Suy luận dựa trên phép thử là tổng số lần chạy trong một mẫu quan sát cung cấp một dấu hiệu về tính ngẫu nhiên của mẫu. Giả thuyết vô hiệu là mô hình của các sự kiện được xác định bởi một quá trình ngẫu nhiên. Có hai giả thuyết thay thế một phía, mẫu này không phải là ngẫu nhiên vì có quá ít hoặc quá nhiều lần chạy được cho là do may rủi. Giả thuyết thay thế hai mặt là mẫu của chạy không phải ngẫu nhiên. Thống kê thử nghiệm là U, tức là số lần chạy. Phân phối mẫu chính xác của U là đã biết. Đối với các mẫu mà tần suất của các sự kiện trong một trong hai loại nhị phân là > 20, một phép xấp xỉ mẫu lớn phân phối mẫu của U có thể được sử dụng. Ví dụ, giả sử tổng số dấu + và – là 44, trong đó 21 dấu + và 23 dấu còn lại -. Số lần chạy bằng 2 và tần suất trong cả hai loại nhị phân là > 20. Trong ví dụ này, phép xấp xỉ mẫu lớn có thể được sử dụng.

3. Giả định kiểm tra

Đây là một bài kiểm tra một mẫu đơn giản với ít giả định, cụ thể là:

• Các quan sát có thể được phân loại là nhị phân (dữ liệu có thể được phân đôi – trên hoặc dưới một giá trị trung vị – median).
• Các quan sát được ghi lại theo trình tự (thứ tự) sự xuất hiện của chúng.

4. Kiểm tra One-sample Runs Test trong SPSS

Một nhà nghiên cứu nghiên cứu về hiệu quả của dự án giảng dạy học phần “Technical Wirting and Presentation” với việc học tiếng Anh chuyên ngành kỹ thuật của sinh viên. Họ thu thập điểm của 50 sinh viên kỹ thuật trong bài kiểm tra cuối kì của học phần đó. Điểm của sinh viên được tính trên thang điểm hệ số 4 (tín chỉ). Điểm số cần đảm bảo được nhập lần lượt theo trình tự chấm bài của giảng viên, nếu không bài kiểm tra Runs test không còn giá trị vì mất đi tính thứ tự (trình tự) của các quan sát. Nhà nghiên cứu có thể quan tâm đến vấn đề điểm số sinh viên có phải là ngẫu nhiên bởi một quá trình chấm điểm ngẫu nhiên bởi giảng viên hay không.

Các bước chạy One-sample Runs Test trong SPSS như sau:

Bước 1. Click Analyze > Nonparametric Tests > Legacy Dialogs > Runs…

Bước 2. Trong hộp thoại Runs Test, chúng ta chuyển các biến cần kiểm tra tính ngẫu nhiên (trong trường hợp này là biến ‘TiengAnh’)vào hộp Test Variables List. Trong vùng Cut Point là các lựa chọn điểm cắt để tạo ra dữ liệu nhị phân cho kiểm định Runs test. Nếu dữ liệu là điểm số, chúng ta có thể chọn điểm cắt là Trung vị (median), Hoặc Trung bình (mean) hoặc một giá trị được thiết lập. Trong ví dụ này, chúng tôi chọn điểm cắt là median (trung bình). Nhấp vào Options, chọn Descriptive để hiển thị mô tả dữ liệu đầu ra. Cuối cùng nhấp OK để chạy kết quả.

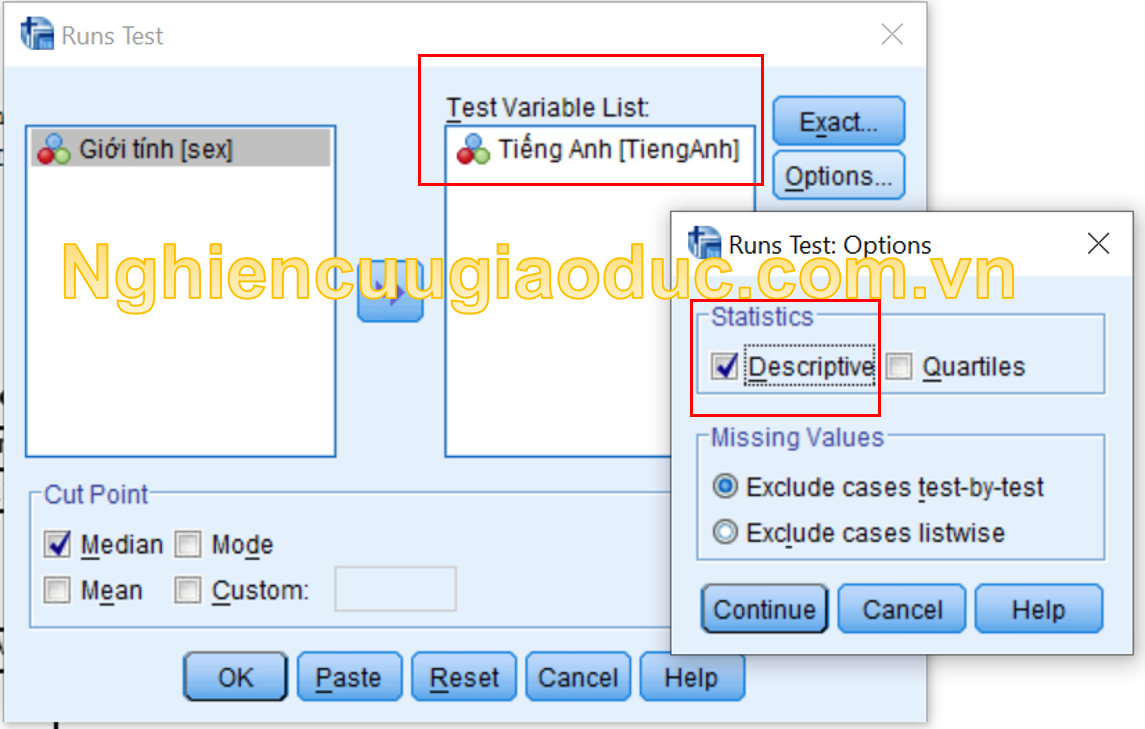
Phân tích kết quả:

Diễn giải kết quả: Một bài kiểm tra One-sample Runs Test với điểm cắt là trung vị (median) cho thấy tổng số trường hợp (total cases) là 50 với số lần chạy = 12 với giá trị kiểm tra là 2 và giá trị Z là -.631. Giá trị Z này có xác suất ý nghĩa là Asymp.sig. (2-tailed) = 0.528. Vì giá trị tuyệt đối của Z ( |Z| ) là .631 nằm trong vùng +/− 1.96; và xác suất này lớn hơn alpha = 0.05 nên chúng ta không thể bác bỏ giả thuyết vô hiệu, điều này có nghĩa rằng các dấu hiệu 1 và 0 xảy ra ngẫu nhiên hay nói cách khác, chuỗi các quan sát xảy ra ngẫu nhiên. Bởi vì bảng Z (vui lòng xem bảng Z tại đây) cho biết tỷ lệ của tổng diện tích dưới đường cong thông thường vượt quá điểm +ve Z, giá trị p liên quan cho Z là 0.631 đối với thử nghiệm hai phía là 0.528 (>0.05).

Tài liệu tham khảo

1. Coolican, H. (2018). Research methods and statistics in psychology. Routledge.
2. Hanneman, R. A., Kposowa, A. J., & Riddle, M. D. (2012). Basic statistics for social research (Vol. 38). John Wiley & Sons.
3. Jackson, S. L. (2015). Research methods and statistics: A critical thinking approach. Cengage Learning.
4. McQueen, R. A., & Knussen, C. (2006). Introduction to research methods and statistics in psychology. Pearson education.
5. Peers, I. (2006). Statistical analysis for education and psychology researchers: Tools for researchers in education and psychology. Routledge.
6. Wagner III, W. E. (2019). Using IBM® SPSS® statistics for research methods and social science statistics. Sage Publications.