Bài 3. Kiểm tra Fisher Exact (Fisher’s Exact Test)

Bài kiểm tra Fisher Exact là kiểm tra có ý nghĩa được sử dụng thay cho kiểm tra chi bình phương trong bảng 2 x 2, đặc biệt trong các trường hợp mẫu nhỏ.

1. Khi nào sử dụng?

Kiểm tra Fisher được sử dụng để kiểm tra ý nghĩa của bất kỳ mối liên hệ hoặc sự khác biệt nào giữa hai mẫu độc lập. Thử nghiệm này xác định xem liệu hai nhóm độc lập có khác biệt đáng kể trong các tỷ lệ các quan sát được phân loại bởi một biến nhị phân phụ thuộc hay không. Giả sử rằng trong tổng số 12 đối tượng nam giới bị chấn thương tay được lấy mẫu. Một nhóm là một mẫu ngẫu nhiên gồm sáu nam giới từ một dân số đã từng bị thương trước tuổi đi học (bị thương khi trẻ dưới 6 tuổi). Mẫu độc lập thứ hai gồm sáu nam giới được chọn từ một dân số đã từng bị thương khi lớn hơn (bị thương khi> 6 tuổi). Biến phụ thuộc là độ thuận tay (trái hoặc phải). Các nhà điều tra có thể muốn biết liệu có bất kỳ mối liên hệ nào giữa tuổi tác khi chấn thương xảy ra và tình trạng thuận tay hay không.

Kiểm định Fisher là một sự thay thế hữu ích cho kiểm tra χ² mẫu r × 2 của mối quan hệ (r×2 sample χ² test of association) khi tổng kích thước mẫu nhỏ, n <20 hoặc khi tần suất kỳ vọng ​​trong bất kỳ ô nào trong bốn ô của bảng phát sinh nhỏ hơn 5. Bài kiểm tra cung cấp một xác suất chính xác cho sự quan sát phân phối tần suất cụ thể trong bảng 2 × 2.

2. Suy luận thống kê và giả thuyết vô hiệu

Các suy luận được thực hiện trong kiểm tra Fisher là về tỷ lệ dân số. Giả thuyết vô hiệu là tỷ lệ trong hai mẫu độc lập là không liên quan với biến nhị phân phụ thuộc. Trong ví dụ về chấn thương tay và thuận tay, giả thuyết vô hiệu sẽ là tuổi khi chấn thương xảy ra độc lập với sự thuận tay.

3. Giả định kiểm tra

Dữ liệu phải là rời rạc (số đếm) và có thể là danh nghĩa (nominal) hoặc thứ tự (ordinal), miễn là các thành viên của mỗi mẫu độc lập có thể được phân loại thành một trong hai nhóm loại trừ lẫn nhau.

4. Kiểm tra Fisher Exact trong SPSS

Bài kiểm tra Fisher Exact tương tự với kiểm tra χ² nhưng sẽ cho kết quả chính xác hơn trong trường hợp cỡ mẫu nhỏ (N<20) hoặc một trong các ô của bảng phát sinh có tần xuất kì vọng nhỏ hơn 5.

– Trường hợp bảng 2×2, kiểm tra Fisher Exact thực hiện đi cùng với kiểm tra χ² và SPSS tự động tính giá trị Fisher Exact bên cạnh giá trị kiểm định χ². Xin vui lòng xem cách thực hiện trong phần kiểm tra χ². Kết quả thu được như hình dưới đây:

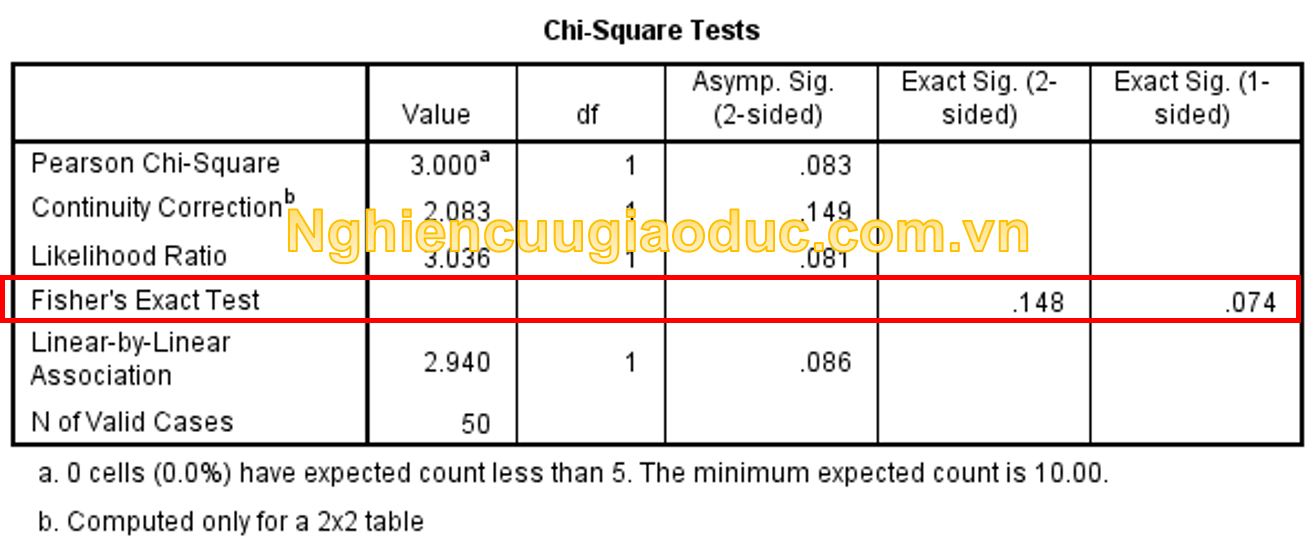
– Trong trường hợp một bảng lớn hơn (chẳng hạn 2×5), nhưng cỡ mẫu nhỏ hoặc tần suất kì vọng của ít nhất 1 ô nhỏ hơn 5 thì khi đó chúng ta cần thực hiện kiểm định Fisher Exact có nút Exact. Trong Exact, hai kỹ thuật được sử dụng bổ sung là Exact và Monte Carlo để đưa ra ý nghĩa thống kê. Nếu sử dụng Monte Carlo, chúng ta cần nhập độ tin cậy và số mẫu được sử dụng trong tính toán. Kỹ thuật Monte Carlo cho kết quả nhanh hơn so với Exact. Nếu sử dụng kỹ thuật Exact, chúng ta cần xác định thời gian tối đa mỗi phép tính toán. Nếu thời gian này trên 30 phút thì nên sử dụng Monte Carlo. Trong phần dưới đây sẽ hướng dẫn thực hiện kiểm tra Fisher Exact.

Ví dụ, một nhà nghiên cứu giáo dục có thể quan tâm đến mối liên hệ giữa biến giới tính và GPA từ dữ liệu thu thập được với 654 sinh viên đại học. Giả thuyết vô hiệu sẽ là giới tính và GPA của các sinh viên là độc lập với nhau.

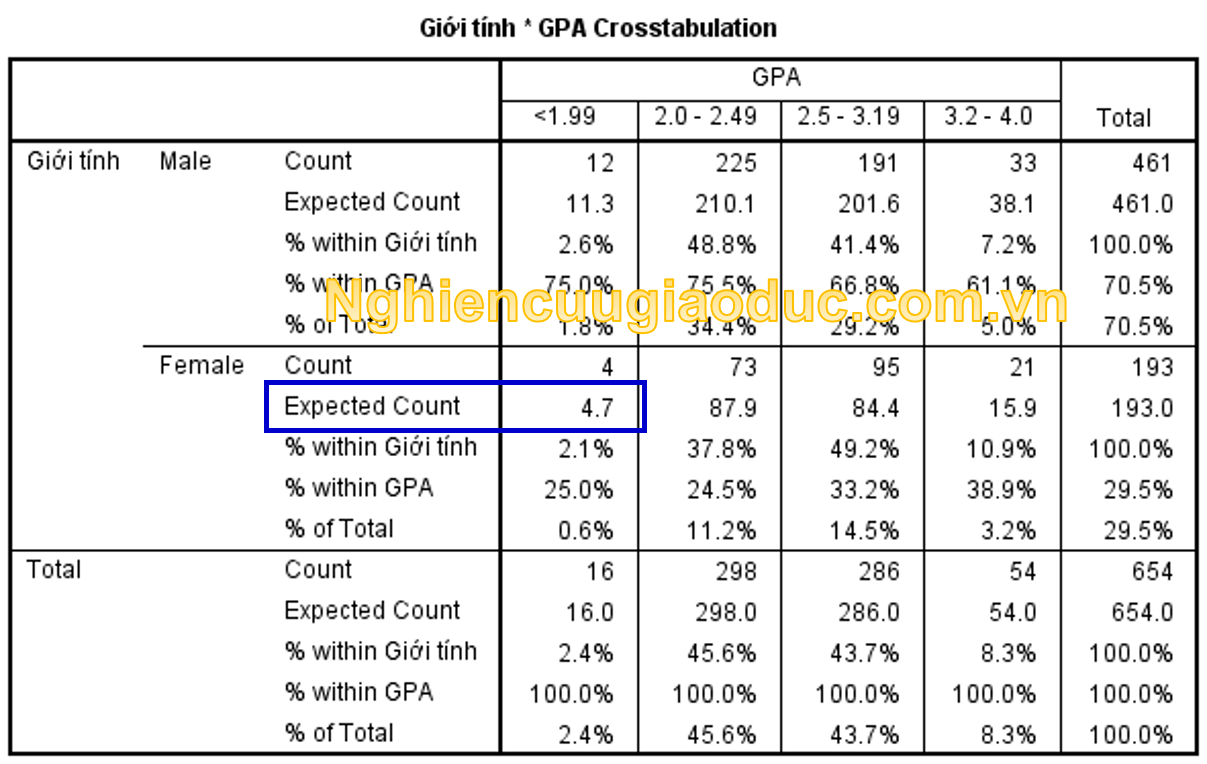
Đầu tiên, chúng ta cần kiểm tra xem dữ liệu có phù hợp để sử dụng với kiểm tra Fisher Exact hay không. Để thực hiện việc, chúng ta chạy bảng CrossTabs như trong kiểm tra χ² với đầy đủ tần suất quan sát và tần suất kì vọng của dữ liệu. Kết quả được hiển thị trong bảng dưới đây:

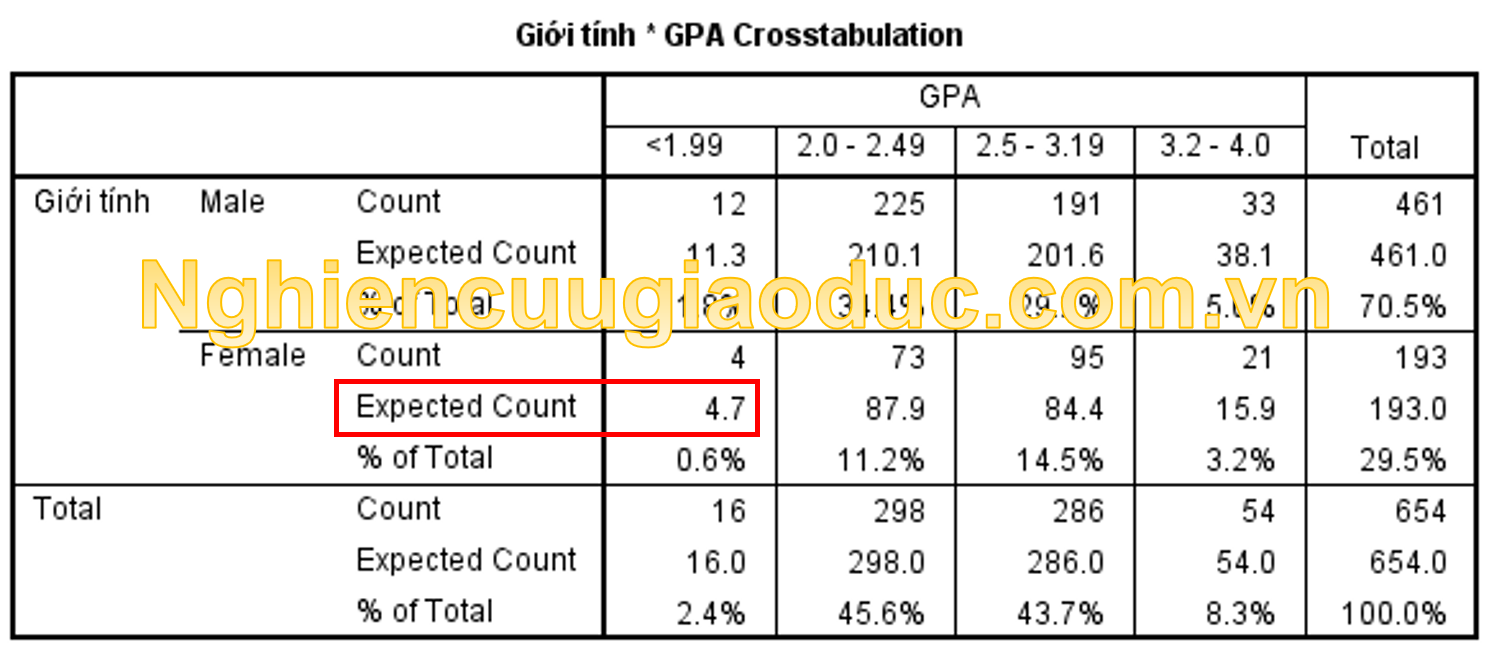
Trong bảng CrossTabs về tần suất bảng 2×4 giữa giới tính và GPA của 654 sinh viên cho thấy ô giá trị kì vọng của sinh viên nữ tương ứng GPA <1.99 bằng 4.7 (tức là nhỏ hơn 5). Khi đó chúng ta cần sử dụng kiểm định Fisher Exact.

Các bước thực hiện như sau:

Bước 1. Vào Analyze > Descriptives Statics > CrossTabs…

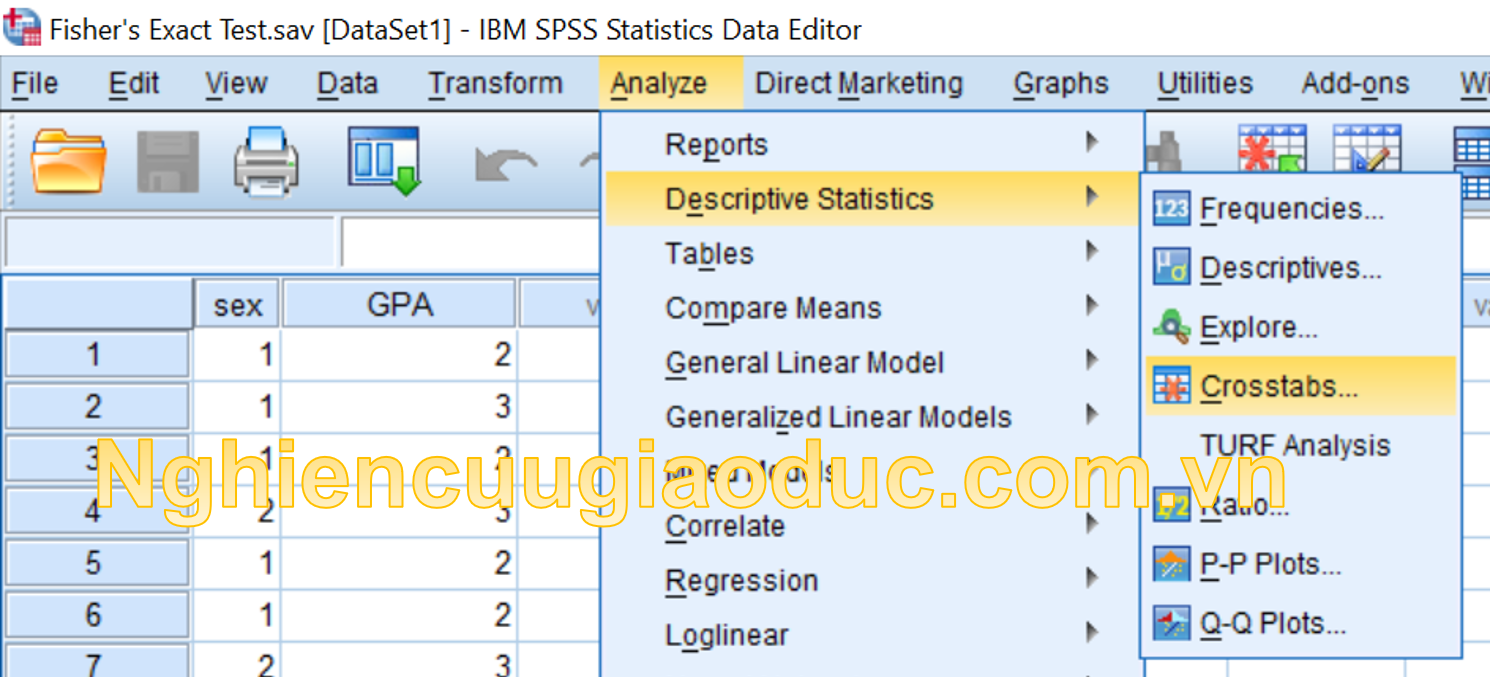
Bước 2. Tại cửa sổ CrossTabs, chúng ta đưa biến giới tính (sex) vào ô Row(s), biến GPA vào ô Column(s). Chúng ta có thể chọn Display Clustered bar charts nếu muốn hiển thị biểu đồ kết quả.

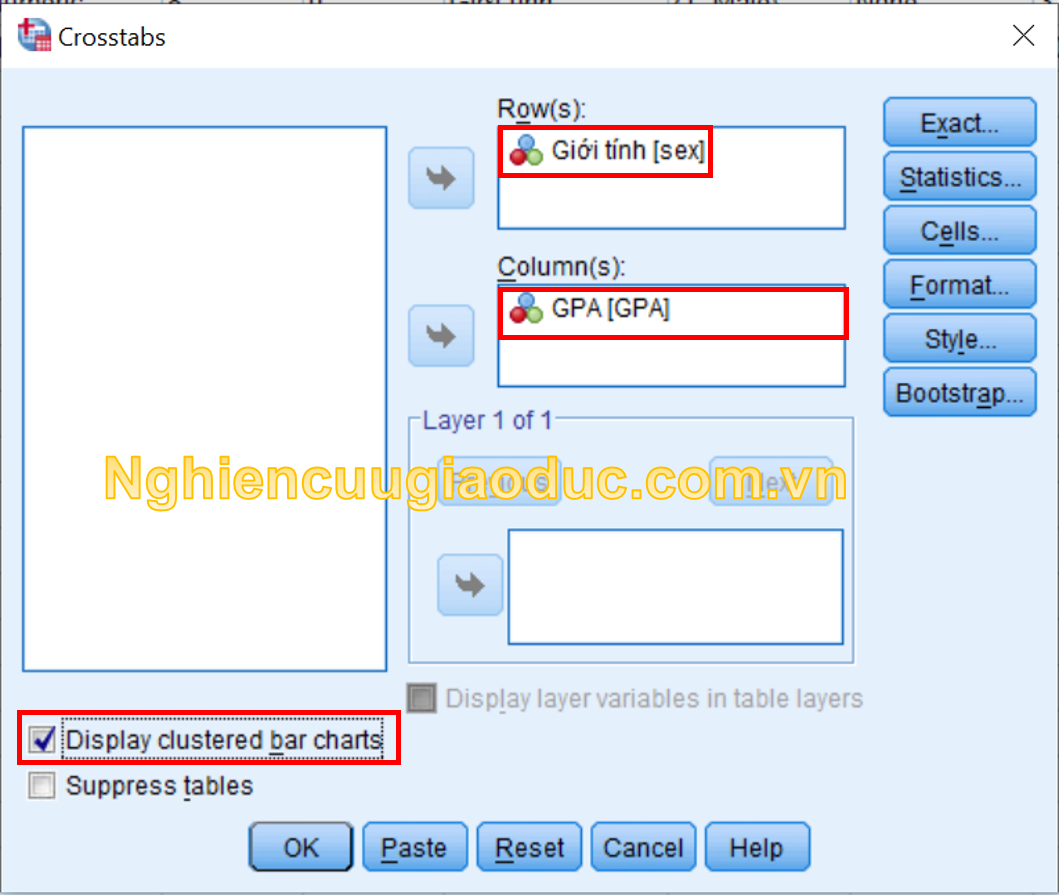
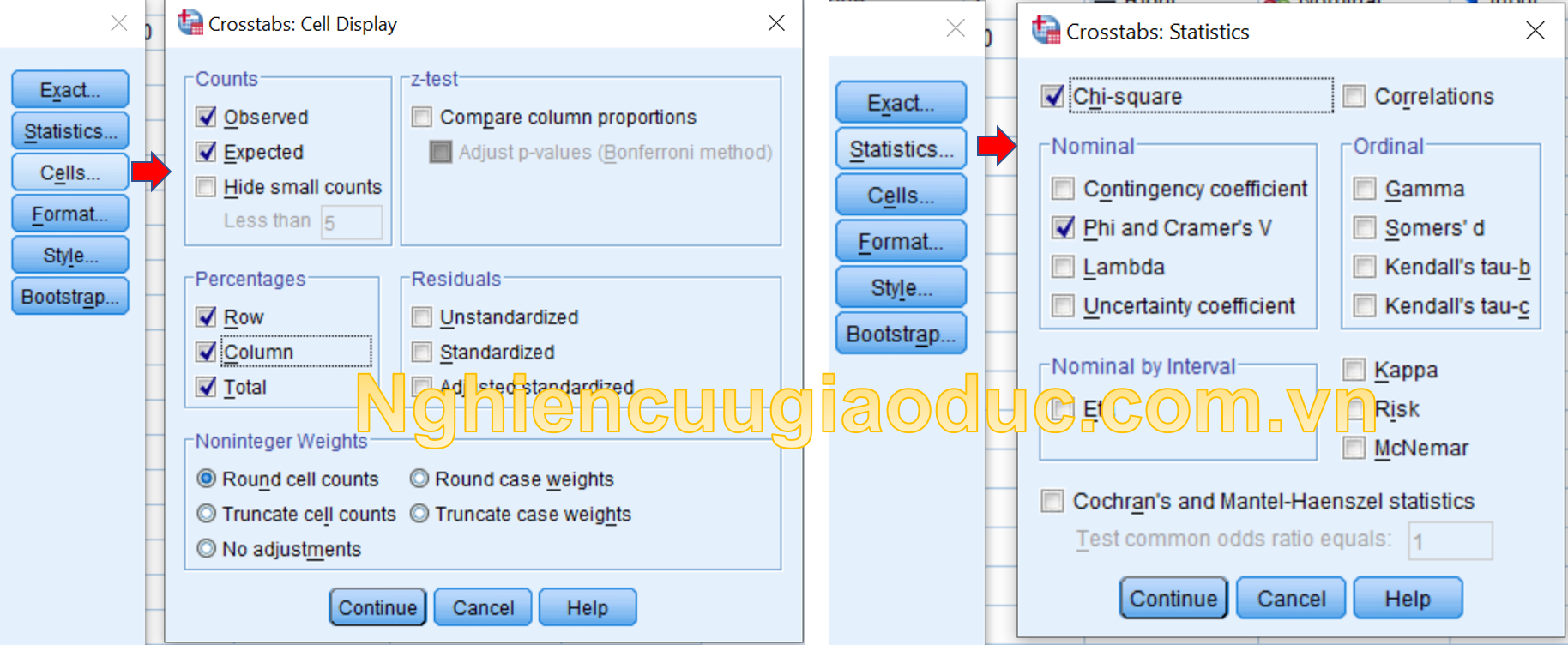
Bước 3. Các thiết lập khác ở nút Statistics và Cells thực hiện như kiểm tra χ². Sau khi thiết lập ở mỗi nút, chúng ta bấm Continue.

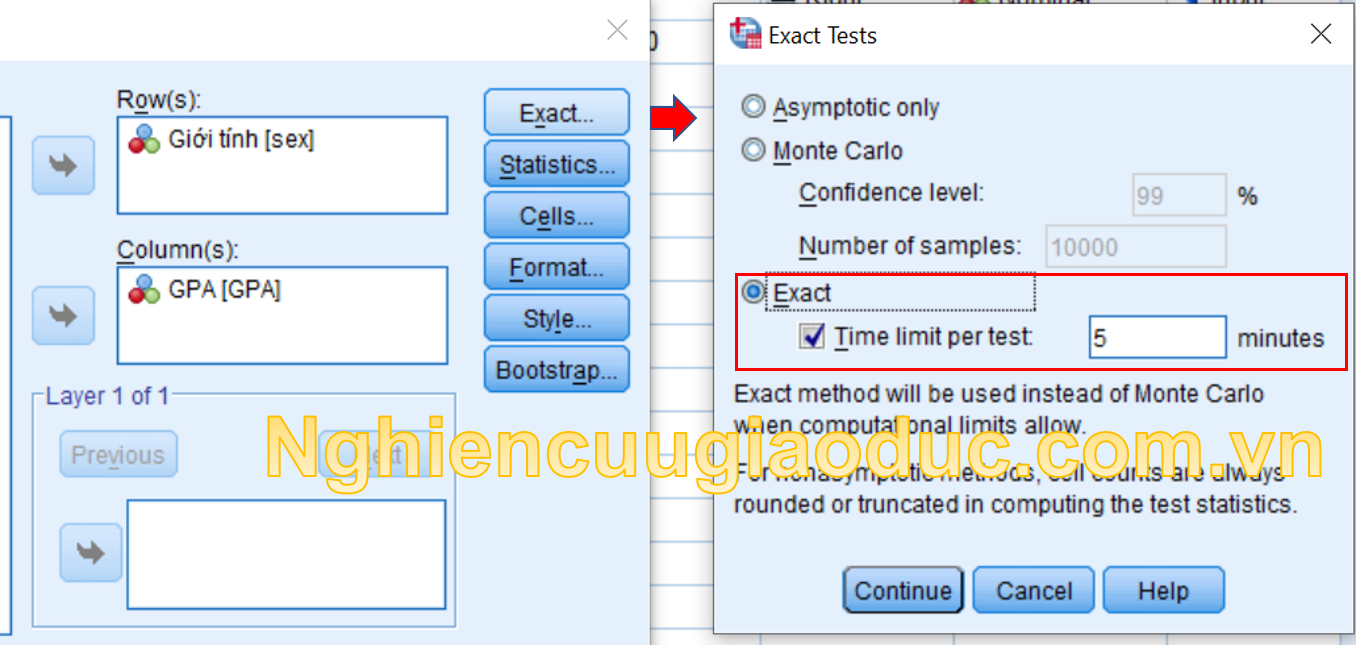
Bước 4. Cuối cùng, tại nút Exact, chúng ta chọn như hình dưới đây, thiết lập thời gian tính toán giới hạn khoảng 5 phút, sau đó bấm Continue và OK để đi đến kết quả.

Phân tích bảng Giới tính * GPA Crosstabulation tương tự như trong kiểm định χ². Vui lòng đọc lại bài kiểm tra χ².

Bảng Chi-Square Tests cung cấp các thông tin quan trọng nhất, kết quả Fisher Exact sẽ có sự khác biệt đôi chút so với kiểm tra χ².

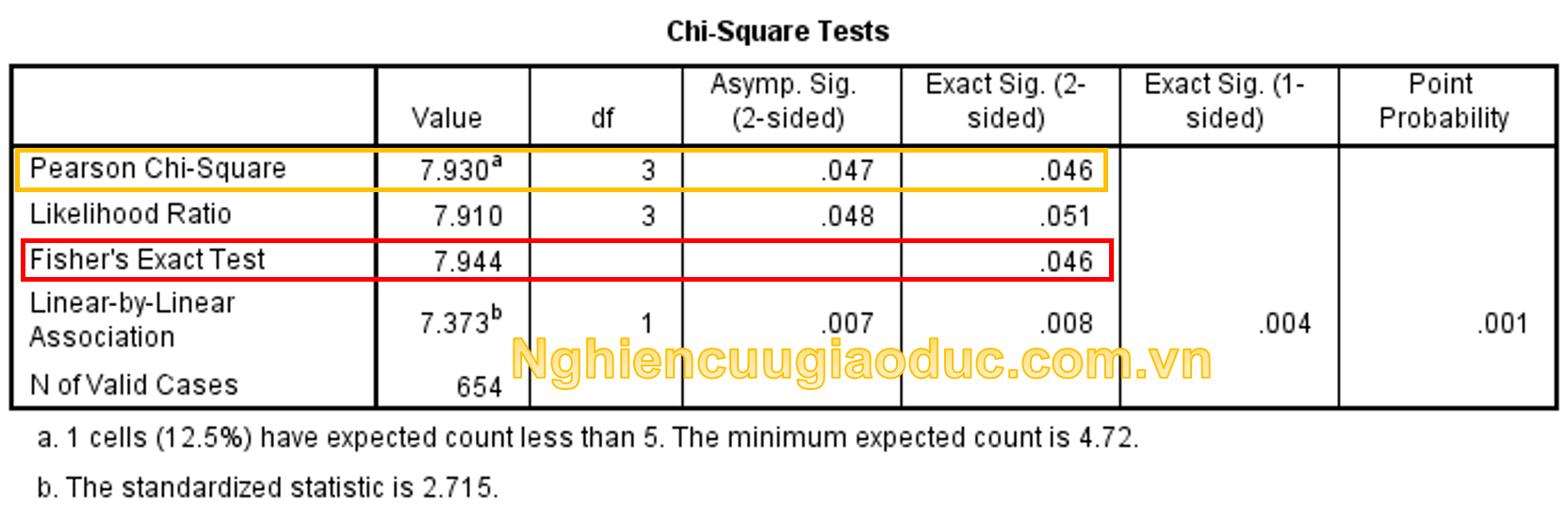
– Mức ý nghĩa Sig. (2-sided) ở hai phương pháp (χ² và Fisher Exact) là không có sự chênh lệch trong SPSS (p=.46) do giới hạn làm tròn 2 số thập phân và cỡ mẫu lớn. Tuy nhiên, khi copy dữ liệu sang Excel và mở rộng số thập phân chúng ta thấy rõ mức ý nghĩa của kiểm định Fisher Exact (p=.4587) là thấp hơn so với mức ý nghĩa của χ² (p=.4629).

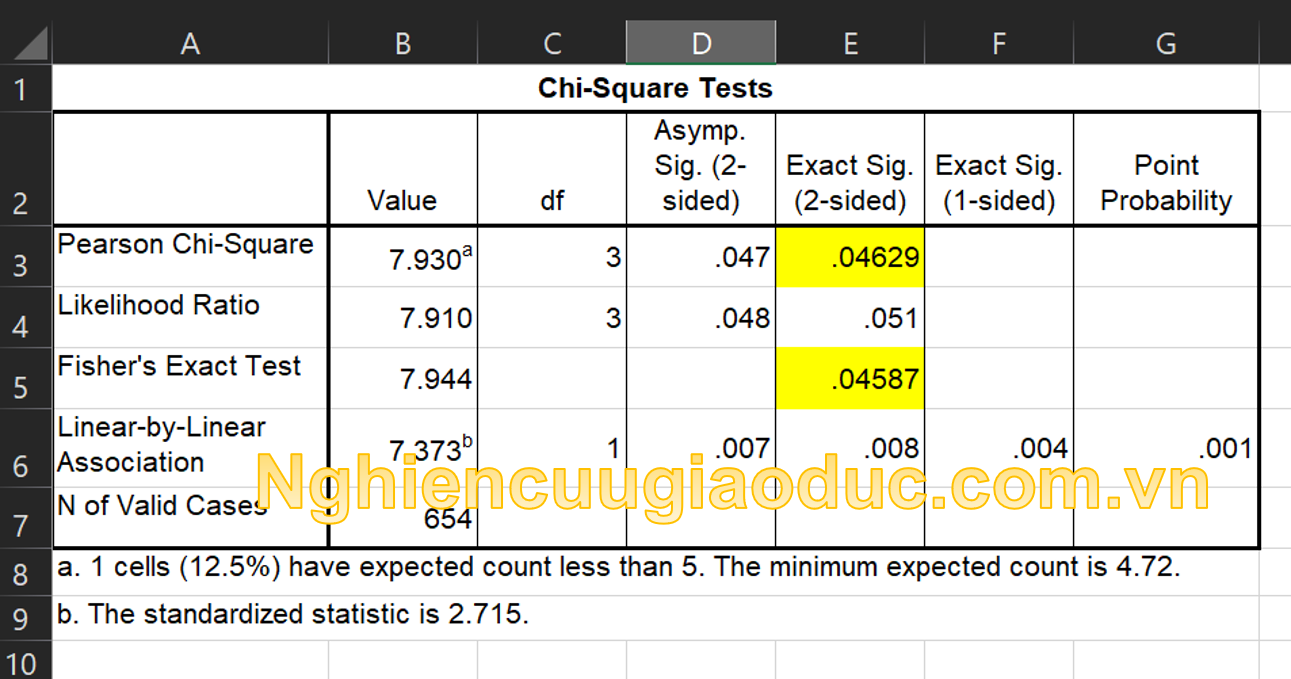
– Sự chênh lệch mức ý nghĩa trong một số trường hợp có thể dẫn đến các kết luận trái ngược nhau về chấp nhận hoặc bác bỏ giả thuyết. Trong trường hợp này, ở mức ý nghĩa p≤0.05 nên chúng ta bác bỏ giả thuyết H₀ và kết luận rằng hai biến giới tính và GPA của các sinh viên đại học là không độc lập với nhau, tức chúng có mối quan hệ với nhau (p = 0.4587).

Tuy nhiên, mối quan hệ giữa hai biến này là yếu do hệ số Carmer’s V là 0.046 (tức là 4.6%, hai biến tương quan thấp).

Chúng ta có thể kết luận trong bài báo: Một bài kiểm tra Fisher Exact đã được thực hiện để kiểm tra liệu có mối liên hệ giữa biến giới tính và GPA từ dữ liệu thu thập được với 654 sinh viên đại học hay không. Kết quả cho thấy mức ý nghĩa p≤0.05 nên chúng ta bác bỏ giả thuyết vô hiệu và kết luận rằng hai biến giới tính và GPA của các sinh viên đại học là không độc lập với nhau, tức chúng có mối quan hệ với nhau (p = 0.4587). Tuy nhiên, mối quan hệ giữa hai biến này là yếu do hệ số Carmer’s V là 0.046 (4,6% tương quan).

Tài liệu tham khảo

1. Coolican, H. (2018). Research methods and statistics in psychology. Routledge.
2. Hanneman, R. A., Kposowa, A. J., & Riddle, M. D. (2012). Basic statistics for social research (Vol. 38). John Wiley & Sons.
3. Jackson, S. L. (2015). Research methods and statistics: A critical thinking approach. Cengage Learning.
4. McQueen, R. A., & Knussen, C. (2006). Introduction to research methods and statistics in psychology. Pearson education.
5. Peers, I. (2006). Statistical analysis for education and psychology researchers: Tools for researchers in education and psychology. Routledge.
6. Wagner III, W. E. (2019). Using IBM® SPSS® statistics for research methods and social science statistics. Sage Publications.