Bài 2. Thiết kế tương quan (Correlational Designs)
Sau khi đọc xong bài này, bạn sẽ có thể:
|
1. Khi nào sử dụng?
Thiết kế tương quan tạo cơ hội cho bạn dự đoán điểm số và giải thích mối quan hệ giữa các biến. Trong thiết kế nghiên cứu tương quan, nhà điều tra sử dụng kiểm định thống kê tương quan để mô tả và đo lường mức độ liên kết (hoặc mối quan hệ) giữa hai hoặc nhiều biến hoặc tập hợp điểm. Trong thiết kế này, các nhà nghiên cứu không cố gắng kiểm soát hoặc thao túng các biến như trong một thử nghiệm; thay vào đó, chúng liên quan, sử dụng thống kê tương quan, hai hoặc nhiều điểm số cho mỗi người (ví dụ như điểm thành tích của học sinh cho mỗi cá nhân).
Nghiên cứu tương quan là gì?
Tương quan (correlation) là một phép thử thống kê để xác định xu hướng hoặc kiểu mẫu cho hai (hoặc nhiều) biến hoặc hai bộ dữ liệu thay đổi nhất quán. Trong trường hợp chỉ có hai biến, điều này có nghĩa là hai biến chia sẻ phương sai chung. Điều đó có nghĩa là chúng ta có thể dự đoán điểm trên một biến với điểm số của cá nhân trên một biến khác. Ví dụ, một nhà nghiên cứu có thể quan tâm đến việc thời gian ôn tập có tương quan với thành tích thi môn Toán của học sinh hay không? Hay nói khác đi, một nghiên cứu tương quan sẽ được tiến hành để đo lường mức độ liên kết giữa thời lượng ôn tập và thành tích thi môn Toán của học sinh. Nếu mối liên hệ được tìm thấy, chúng ta hoàn toàn có thể dự đoán được điểm trung bình của thành tích thi toán bằng số giờ ôn tập của học sinh, hoặc ngược lại.
Khi nào sử dụng nghiên cứu tương quan?
Bạn sử dụng thiết kế này khi tìm kiếm sự liên hệ giữa hai hoặc nhiều biến để xem liệu chúng có ảnh hưởng lẫn nhau hay không. Thiết kế này cho phép bạn dự đoán một kết quả, chẳng hạn như dự đoán rằng thời lượng ôn tập ảnh hưởng đến thành tích thi của học sinh.
2. Các loại thiết kế tương quan
Hai thiết kế tương quan chính là giải thích (explanation) và dự đoán (prediction).
2.1. Thiết kế giải thích (Explanatory Design)
Nghiên cứu tương quan giải thích (explanatory correlational research) có một mục tiêu cơ bản là giải thích mối liên hệ giữa hoặc giữa các biến. Một thiết kế nghiên cứu giải thích (explanatory research design) là một thiết kế tương quan, trong đó nhà nghiên cứu quan tâm đến mức độ mà hai biến (hoặc nhiều) đồng biến đổi, nghĩa là khi những thay đổi của một biến được phản ánh trong những thay đổi của biến kia. Thiết kế giải thích xem xét một sự liên kết đơn giản giữa hai biến (ví dụ như thời gian ôn tập và thành tích thi) hoặc nhiều hơn hai (ví dụ: mối liên hệ giữa trầm cảm, lo lắng và stess của các sinh viên).
2.2. Thiết kế dự đoán (Prediction Design)
Trong thiết kế dự đoán, các nhà nghiên cứu tìm cách dự đoán kết quả bằng cách sử dụng các biến nhất định. Ví dụ, thời gian ôn tập có dự đoán trước điểm số thành tích học tập của học sinh hay không. Do đó, các nghiên cứu dự đoán là rất hữu ích vì chúng giúp đoán trước (anticipate) hành vi trong tương lai.
Mục đích của một thiết kế nghiên cứu dự đoán (prediction research design) là xác định các biến sẽ dự đoán một kết quả. Kết quả được dự đoán trong nghiên cứu tương quan được gọi là biến phản hồi. Trong hình thức nghiên cứu này, nhà nghiên cứu xác định một hoặc nhiều biến dự đoán (còn được gọi là biến giải thích) và một biến kết quả (hoặc biến phản hồi). Biến dự đoán (predictor variable) là một biến được sử dụng để đưa ra dự báo về một kết quả trong nghiên cứu tương quan. Trong trường hợp dự đoán điểm số thành tích học tập bằng thời gian ôn tập, người dự đoán có thể khuyến cáo học sinh về thời gian ôn tập cần thiết.
Một nghiên cứu dự đoán sẽ báo cáo các mối tương quan bằng cách sử dụng các kiểm tra thống kê tương quan, nhưng nó có thể bao gồm các thủ tục thống kê nâng cao. Ví dụ, tác giả có thể quan tâm đến một số yếu tố dự báo giúp giải thích biến phản hồi. Mặc dù hồi quy tuyến tính đơn giản giải quyết mối quan tâm này, nhưng hồi quy bội cung cấp một công thức phức tạp hơn.
3. Các đặc điểm chính của thiết kế tương quan
Các nghiên cứu tương quan bao gồm các đặc điểm cụ thể: i) Hiển thị điểm số (đồ thị phân tán và ma trận tương quan), ii) Mối liên kết giữa các điểm số (hướng, hình thức và sức mạnh), iii) Phân tích đa biến (tương quan từng phần và hồi quy bội).
3.1. Hiển thị điểm số với đồ thị phân tán hoặc ma trận tương quan
Nếu bạn có hai tập điểm, trong nghiên cứu tương quan, bạn có thể vẽ các điểm này trên một đồ thị phân tán hoặc trình bày chúng trong một bảng ma trận tương quan.
i) Đồ thị phân tán (Scatterplot)
Các nhà nghiên cứu vẽ đồ thị điểm số cho hai biến số trên một biểu đồ để cung cấp một bức tranh trực quan về hình thức của các điểm số. Điều này cho phép các nhà nghiên cứu xác định loại liên kết giữa các biến và xác định các điểm cực trị. Quan trọng nhất, biểu đồ này có thể cung cấp thông tin hữu ích về hình thức (form) của liên kết – có thể là tuyến tính (theo đường thẳng) hay cong. Nó cũng cho biết hướng (direction) của sự liên kết (ví dụ: một điểm số tăng lên và điểm số khác cũng tăng lên) và mức độ (degree) của sự liên kết (ví dụ, mối tương quan là hoàn hảo sẽ có giá trị bằng 1.0).
Một đồ thị phân tán giúp đánh giá mối liên quan giữa hai điểm số cho những người tham gia. Các điểm số này thường được xác định là X và Y, với các giá trị X được biểu thị trên trục hoành và các giá trị Y được biểu thị trên trục tung. Một điểm đơn lẻ cho biết điểm X và Y giao nhau ở đâu cho một cá nhân.
Hình 1: Đồ thị phân tán giữa thành tích thi Toán và thời lượng ôn tập (giờ)

Ví dụ, đồ thị phân tán của các điểm số trong Hình 1 cho thấy một đồ thị trực quan về mối liên kết giữa thành tích thi toán (điểm thi) và thời lượng ôn tập của học sinh. Giả sử rằng nhà nghiên cứu tương quan tìm cách nghiên cứu xem thành tích thi Toán có liên quan đến thời lượng ôn tập hay không. Chúng ta có thể cho rằng những học sinh có số giờ ôn tập cao thì có khả năng đạt được một điểm số cao hơn về thành tích thi. Đám mây ma trận điểm số biểu thị một đường thẳng về mối quan hệ tuyến tính giữa hai điểm số.
ii) Ma trận tương quan (Correlation Matrix)
Các nhà nghiên cứu tương quan thường trình bày các hệ số tương quan trong ma trận. Ma trận tương quan hiển thị trực quan các hệ số tương quan cho tất cả các biến trong một nghiên cứu. Trong hiển thị này, chúng ta liệt kê tất cả các biến trên cả hàng ngang và cột dọc trong bảng. Hệ số tương quan được hiển thị trong các ô là sự giao nhau giữa hàng ngang và cột dọc, biểu thị cho mối liên kết giữa hai biến.
Bảng 1: Ma trận tương quan giữa thành tích thi Toán và thời lượng ôn tập (giờ)
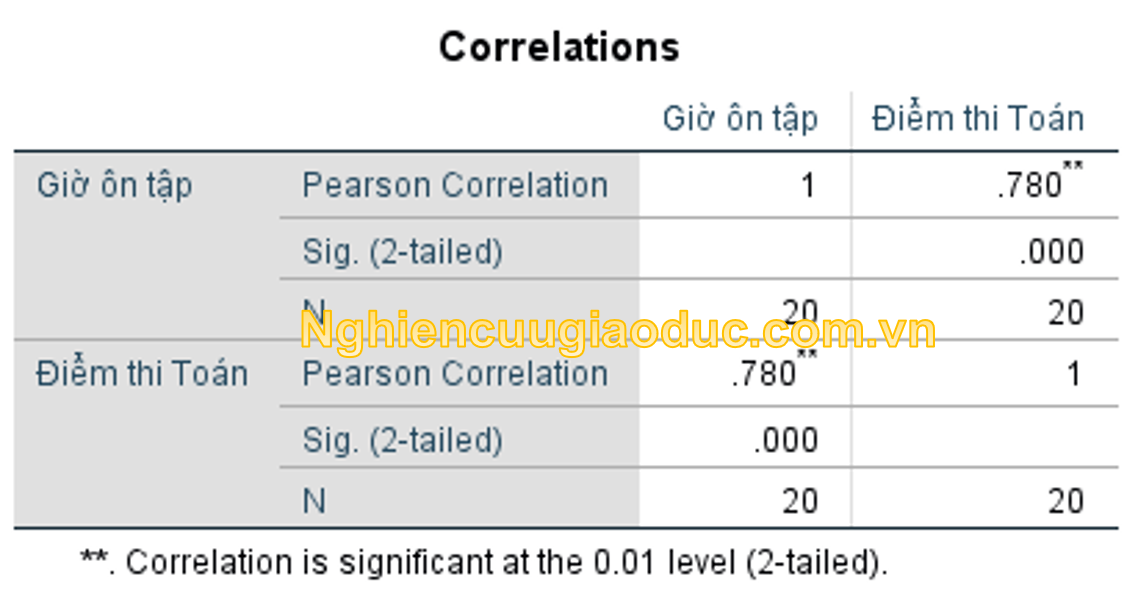
Ví dụ về một ma trận tương quan được thể hiện trong Bảng 1, một hệ số tương quan được báo cáo là 0.78 (tại mức alpha 0.01) biểu thị mức độ của mối liên kết giữa hai biến ‘điểm thi Toán’ và ‘Giờ ôn tập’ của học sinh. Chú ý rằng các dấu hoa thị (*) cho biết liệu hệ số tương quan có ý nghĩa thống kê ở mức p < 0.05 và p < 0.01 hay không.
3.2. Mối liên kết giữa các điểm số
Sau khi các nhà nghiên cứu tương quan vẽ đồ thị các điểm số và tạo ra một ma trận tương quan, sau đó họ có thể giải thích ý nghĩa của mối liên hệ giữa các điểm số. Điều này đòi hỏi bạn phải hiểu hướng của mối liên kết, hình thức của phân phối, mức độ của liên kết và sức mạnh của nó.
i) Hướng của mối liên kết
Khi xem xét một đồ thị, điều quan trọng là phải xác định xem các điểm cắt nhau, hoặc di chuyển theo cùng hướng hay ngược chiều. Trong mối tương quan thuận, các điểm di chuyển theo cùng một hướng; nghĩa là, khi X tăng thì Y cũng tăng, hoặc ngược lại, nếu X giảm, thì Y cũng vậy. Trong mối tương quan nghịch (được biểu thị bằng hệ số tương quan “-”), các điểm di chuyển theo hướng ngược lại; nghĩa là khi X tăng thì Y giảm và khi X giảm thì Y tăng. Nếu điểm trên một biến không liên quan theo bất kỳ hình mẫu nào trên biến kia, thì không tồn tại mối quan hệ tuyến tính.
ii) Hình dạng của mối liên kết
Các nhà nghiên cứu tương quan xác định dạng của điểm số được vẽ là tuyến tính hoặc phi tuyến tính. Nếu mối liên kết được xác định là tuyến tính thì nó tồn tại trong hai hình thức: 1) mối quan hệ tuyến tính dương (positive linear relationship), và 2) mối quan hệ tuyến tính âm (negative linear relationship). Trong trường hợp này, hệ số tương qua Pearson (kí hiệu là r) sẽ được tính toán.
Nếu phân phối đường cong (hoặc mối quan hệ phi tuyến) cho thấy mối liên kết hình chữ U trong điểm số. Trong trường hợp này, nếu hệ số tương quan Pearson được sử dụng, nó sẽ cung cấp một đánh giá thấp hơn về mối tương quan. Do đó, các nhà nghiên cứu sử dụng một thủ tục thống kê khác với ‘r’ để tính toán mối liên kết giữa các biến cho phân phối đường cong và cho cả dữ liệu được xếp hạng liên quan.
Thay vì hệ số tương quan ‘r’, các nhà nghiên cứu sử dụng hệ số tương quan Spearman rho (rs) cho dữ liệu phi tuyến và cho các loại dữ liệu khác được đo trên thang đo phân loại (có xếp hạng). Khi bạn đo lường một biến trên thang đo liên tục (khoảng hoặc tỷ lệ) và biến kia là thang đo phân loại, phân đôi, thống kê tương quan không phải là ‘r’ mà là tương quan lưỡng điểm (point-biserial correlation).
iii) Mức độ và sức mạnh của mối liên kết
Mức độ của mối liên kết (Degree of association) có nghĩa là sự liên kết giữa hai biến là hệ số tương quan từ -1.00 đến +1.00, với 0.00 cho thấy không có liên kết tuyến tính nào cả. Nó giúp các nhà nghiên cứu giải thích độ lớn và hướng của các mối tương quan giữa hai biến.
Mặc mối tương quan phản ánh mức độ của mối liên kết (Degree of association), nhưng nhiều nhà nghiên cứu thích bình luận về giá trị bình phương mối tương quan ‘r2’ và sử dụng giá trị kết quả để đo độ mạnh của mối quan hệ. Trong thủ tục này, các nhà nghiên cứu tính toán một ‘hệ số xác định’ (coefficient of determination), hệ số này đánh giá tỷ lệ biến thiên trong một biến có thể được xác định hoặc giải thích bởi biến thứ hai. Ví dụ: nếu bạn nhận được r = 0.70 (hoặc -0.70), bình phương giá trị này dẫn đến r2 = 0.49 (hoặc 49%). Điều này có nghĩa là gần một nửa (49%) sự thay đổi trong Y có thể được xác định hoặc giải thích bởi X. Trong ví dụ của chúng ta (Hình 1), chúng ta có thể nói rằng thời lượng ôn tập giải thích cho 60.8% điểm thành tích thi Toán của học sinh (r2 = 0.608).
Ngoài ra, cũng có các tiêu chuẩn khác để giải thích sức mạnh của mối liên kết. Một hướng dẫn như vậy có sẵn trong Cohen (2013). Hãy xem xét các diễn giải sau với kích thước của hệ số tương quan:
- Từ 0.20 – 0.35: một mối quan hệ nhỏ; mối quan hệ này có thể hơi có ý nghĩa thống kê.
- Từ 0.35 – 0.65: mối tương quan hữu ích cho việc dự đoán hạn chế.
- Từ 0.66 – 0.85: mối tương quan dự đoán tốt có thể đưa kết quả từ biến này sang biến khác. Hệ số tương quan trong phạm vi này sẽ được coi là rất tốt.
- Từ 0.86 trở lên: Khi hai hoặc nhiều biến có liên quan với nhau, các mối tương quan cao đến mức này hiếm khi đạt được và nếu chúng dẫn đến kết quả, thì hai biến thực sự đo lường cùng một đặc điểm cơ bản và có lẽ nên được kết hợp trong phân tích dữ liệu.
3.3. Phân tích đa biến (Multiple Variable Analysis)
Trong nhiều nghiên cứu tương quan, các nhà nghiên cứu dự đoán kết quả dựa trên nhiều hơn một biến dự báo. Vì vậy, họ cần phải tính đến tác động của từng biến. Hai cách tiếp cận phân tích nhiều biến là tương quan từng phần (partial correlation) và hồi quy bội (multiple regression).
i) Tương quan từng phần (partial correlation)
Trong nhiều tình huống nghiên cứu, chúng ta nghiên cứu ba, bốn hoặc năm biến như những yếu tố dự báo kết quả. Loại biến được gọi là biến trung gian hoặc biến can thiệp (mediating or intervening variable) đứng giữa các biến độc lập và phụ thuộc và ảnh hưởng đến cả hai biến này. Chúng ta sử dụng các tương quan từng phần để xác định lượng phương sai, nghĩa là một biến can thiệp giải thích trong cả biến độc lập và biến phụ thuộc.
ii) Hồi quy bội (Multiple Regression)
Các nhà nghiên cứu tương quan sử dụng thống kê tương quan để dự đoán điểm số trong tương lai. Để xem tác động của nhiều biến đối với một kết quả, các nhà nghiên cứu sẽ sử dụng mô hình hồi quy tuyến tính bội.
Chúng ta có thể tính toán hệ số hồi quy cho từng biến, đánh giá mức độ ảnh hưởng tổng hợp của tất cả các biến và cung cấp bức tranh về kết quả. Một bảng hồi quy cho thấy tổng phương sai được giải thích trong một biến phụ thuộc bởi tất cả các biến độc lập, được gọi là R2 (R bình phương). Nó cũng thể hiện các trọng số hồi quy (regression weight) – lượng của đóng góp của mỗi biến kiểm soát cho phương sai của tất cả các biến khác, được gọi là beta – cho mỗi biến.
Trọng số beta (beta weight) là hệ số thể hiện độ lớn của dự đoán cho một biến sau khi loại bỏ hiệu ứng của tất cả các yếu tố dự báo khác. Hệ số của trọng số beta xác định mức độ mạnh mẽ của mối quan hệ của một biến dự báo với các kết quả và cho phép nhà nghiên cứu so sánh độ mạnh của một biến dự báo với độ mạnh của các yếu tố dự báo khác. Các hệ số hồi quy chuẩn hóa (Standardized regression coefficient) thường được sử dụng cho các mục đích như lựa chọn các biến và đánh giá tầm quan trọng tương đối của chúng. Trọng số beta được báo cáo ở dạng chuẩn hóa, điểm z chuẩn hóa các thước đo để tất cả các biến có thể được so sánh và được hiểu giống như Pearson r, với giá trị thường từ +1.00 đến -1.00. Lưu ý rằng các bảng hồi quy thường báo cáo giá trị B (một hệ số không chuẩn), nhưng các giá trị này, mặc dù hữu ích trong công thức dự đoán, nhưng không cho phép các nhà nghiên cứu so sánh độ mạnh tương đối của từng biến độc lập như một yếu tố dự đoán vì giá trị có thể được tính điểm trong các đơn vị khác.




















