Bài 7. Thống kê mô tả (Descriptive Statistics)
3. Đo lường sự phân tán (Dispersion)
Để mô tả một phân bố, chúng ta cần một thước đo về sự lan truyền hoặc phân tán của các giá trị cũng như các thước đo về vị trí và hình dạng trung tâm. Số liệu thống kê phổ biến cho biết sự phân tán của các giá trị là phạm vi (range), phạm vi liên tứ phân vị (inter-quartile range) và độ lệch chuẩn (standard deviation).
- Phạm vi là sự khác biệt giữa các giá trị lớn nhất và nhỏ nhất trong một phân phối.
- Phạm vi liên tứ phân vị là một thước đo phân tán truyền tải nhiều thông tin hơn về sự lan truyền của điểm số. Nó được tính bằng hiệu số của giá trị tứ phân vị thứ ba và tứ phân vị thứ nhất (Q3-Q1). Xem hình dưới đây và vui lòng đọc Bài 5- Đồ thị hộp và râu để xem giải thích về phạm vi liên tứ phân vị.

+ Để tính tứ phân vị thấp cho dữ liệu, trước tiên chúng ta cần chia n cho 4. Khi n/4 là một số nguyên, tứ phân vị là giá trị trung bình của hai giá trị ở độ sâu n/4 và độ sâu (n/4 +1). Tứ phân vị trên được tìm thấy bằng cách đếm ngược từ giá trị cao nhất và phần tư dưới được tìm thấy bằng cách đếm ngược từ giá trị thấp nhất.
+ Khi n/4 không phải là số nguyên, các tứ phân vị là giá trị có độ sâu là số nguyên tiếp theo lớn hơn n/4. Chẳng hạn, n = 114 chia cho 4 = 28.5 không phải là số nguyên, số nguyên tiếp theo lớn hơn 28.5 là 29. Các tứ phân vị là ở giá trị thứ 29 tính từ các cực trị của phân phối.
- Độ lệch chuẩn – một phép đo sự phân tán được sử dụng rộng rãi nhất. Thống kê này đo lường sự phân tán của điểm số xung quanh giá trị trung bình. Nếu tất cả các giá trị trong một phân phối đều giống nhau, mỗi giá trị sẽ bằng trung bình, sẽ không có sự phân tán và không giá trị nào lệch khỏi giá trị trung bình và độ lệch chuẩn sẽ bằng không. Càng nhiều giá trị lệch khỏi trung bình, nghĩa là sự biến thiên xung quanh giá trị trung bình càng lớn, thì độ lệch chuẩn càng lớn. Một độ lệch chuẩn của mẫu được tính thông qua phương sai mẫu:
- Phương sai, S2 của n quan sát x1, x2…, xn là:
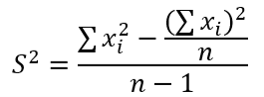
- Độ lệch chuẩn, S, là căn bậc hai của phương sai.
4. Bậc tự do
Trong công thức tính phương sai (hoặc độ lệch chuẩn), bạn có thể thắc mắc tại sao mẫu số lại là n−1. Độ lệch chuẩn thể hiện độ lệch trung bình của mỗi giá trị tạo thành trung bình. Khi chúng ta tính giá trị trung bình, chúng ta chia cho n, tổng của tất cả các giá trị. Đối với độ lệch chuẩn, chúng ta chia cho n−1 vì tổng độ lệch, (trung bình-xi) luôn bằng 0. Do vậy, độ lệch cuối cùng có thể được tìm thấy khi chúng ta biết n−1 độ lệch đầu tiên vì tất cả độ lệch tổng bằng 0. Chỉ n−1 trong số các độ lệch bình phương có thể thay đổi tự do (giá trị cuối cùng là cố định) và do đó chúng ta lấy giá trị trung bình bằng cách chia tổng cho n−1. Chúng ta gọi số n−1 là bậc tự do (df) của một thống kê.
Hãy xem xét ví dụ về sự phân phối điểm số (3, 7, 11). Giá trị trung bình là 7. Hãy xem điều gì sẽ xảy ra nếu bất kỳ hai độ lệch nào (xi – x̅) được tính:
| (xi | x̅ | (xi – x̅) |
| 3 | 7 | -4 |
| 7 | 7 | 0 |
| 11 | 7 | ? |
| Tổng = 0 |
Độ lệch thứ ba phải là +4 vì tổng độ lệch so với giá trị trung bình luôn bằng không. Theo nghĩa này, độ lệch cuối cùng không tự do thay đổi. Biết n − 1 độ lệch, độ lệch cuối cùng có thể được xác định. Do đó, chỉ có n-1 độ lệch là tự do thay đổi và nhận bất kỳ giá trị nào. Như vậy, số bậc tự do của độ lệch chuẩn của mẫu (hoặc phương sai của mẫu) là df = n − 1, trong đó n là số điểm xi trong mẫu.




















