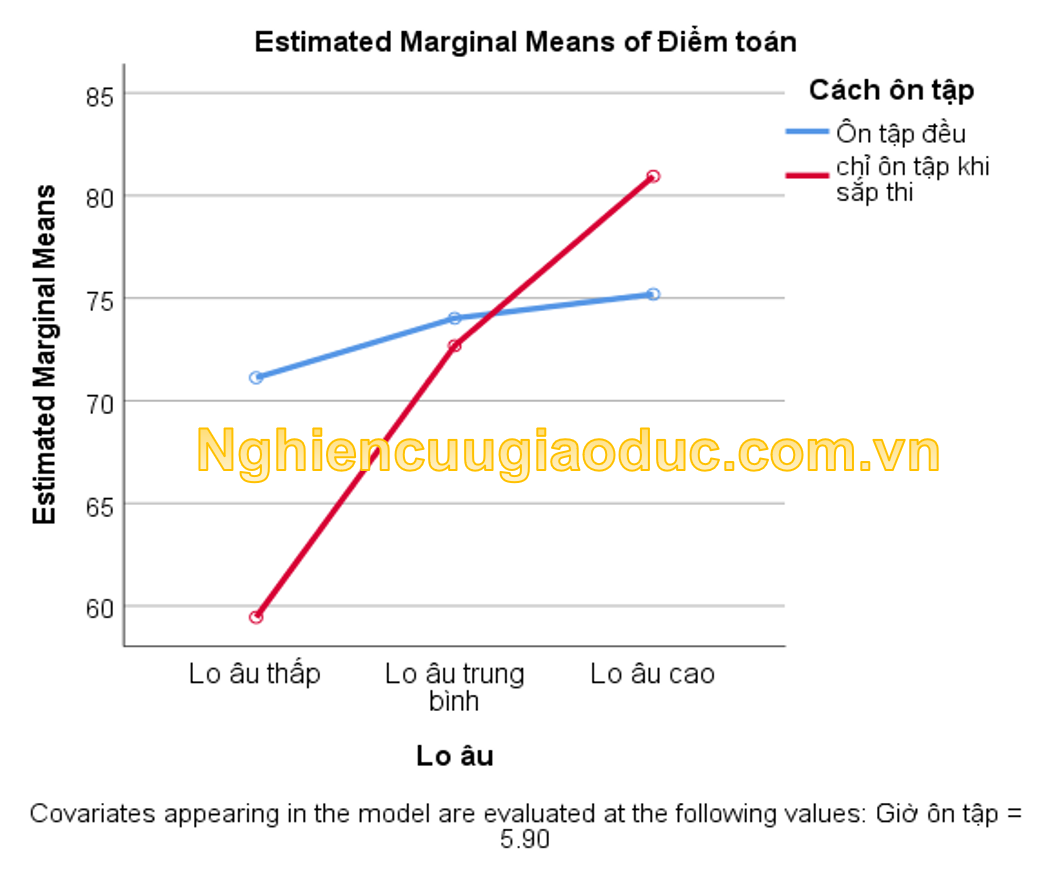
Bài 2. Phân tích phương sai đa biến hai chiều (Two-way MANOVA)
3. Kiểm tra MANOVA hai chiều trong SPSS
Ví dụ, một nhà nghiên cứu muốn kiểm tra xem liệu yếu tố khu vực sống (thành thị, nông thôn, vùng sâu vùng xa) và giới tính (nam và nữ) có ảnh hưởng đến điểm thi tốt nghiệp phổ thông khối D của các môn Toán, Ngữ văn và Tiếng Anh hay không? Nhà nghiên cứu đã tuyển ngẫu nhiên 12 học sinh nam và 12 học sinh nữ, sau đó thu thập điểm thi tốt nghiệp phổ thông của các môn Toán, Ngữ văn và Tiếng Anh. Do đó, ba biến phụ thuộc là điểm thi Toán, Ngữ văn và Tiếng Anh, hai biến độc lập là giới tính và khu vực sống.
Giả thuyết vô hiệu là yếu tố khu vực sống và giới tính, và hiệu ứng tương tác giữa chúng là không ảnh hưởng đến điểm thi tốt nghiệp toán, ngữ văn và tiếng Anh. Yếu tố hiệu ứng tương tác thường được ưu tiên đầu tiên trong phân tích MANOVA hai chiều vì kết quả của nó sẽ xác định cách tiếp theo phân tích MANOVA hai chiều và đảm bảo rằng kết quả của bạn không bị sai lệch hoặc không đầy đủ. Giả sử rằng một hiệu ứng tương tác có ý nghĩa thống kê được tìm thấy, điều này cho thấy rằng ba khu vực sống có tác động khác nhau ở học sinh nam và học sinh nữ (nghĩa là, ảnh hưởng của ba khu vực sống đối với điểm Toán, điểm Văn và điểm Anh phụ thuộc vào giới tính của học sinh). Việc bạn có tìm thấy một tương tác có ý nghĩa thống kê hay không sẽ xác định những hiệu ứng nào trong MANOVA hai chiều mà bạn nên diễn giải và những phân tích tiếp theo mà bạn có thể muốn chạy. Mức ý nghĩa Alpha được chọn là 5%.
3.1. Kiểm tra giả định
Trước khi thực hiện bài kiểm tra MANOVA hai chiều, chúng ta cần tiến hành các bài kiểm tra một số giả định cơ bản. Xin vui lòng đọc phần kiểm tra giả thuyết trong bài MANOVA một chiều để xem cách kiểm tra giả định.
a) Để kiểm tra giả định 7 về mối quan hệ tuyến tính giữa từng cặp biến phụ thuộc cho mỗi nhóm của biến độc lập, bạn có thể kiểm tra giả định này bằng cách vẽ một đồ thị ma trận phân tán (vui lòng đọc bài đồ thị ma trận phân tán và vẽ đồ thị với ba biến Điểm Toán, Điểm Văn và Điểm Anh cho mỗi nhóm của biến độc lập). Kết quả thu được như hình dưới đây:
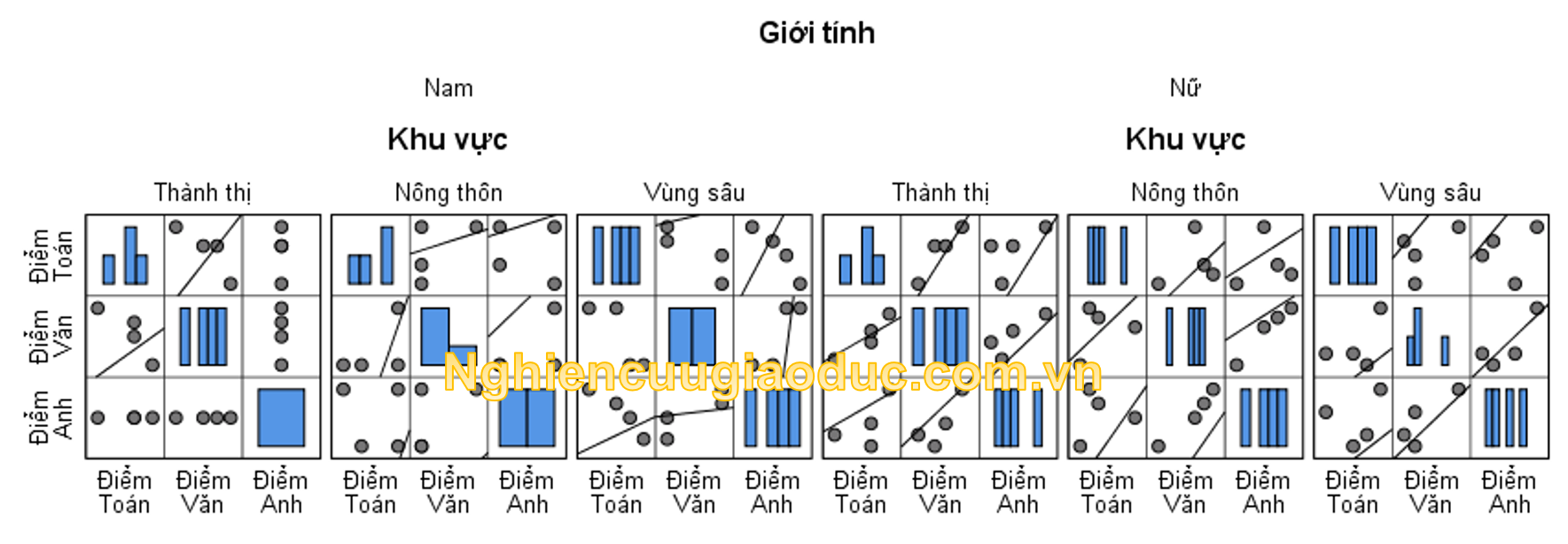
Nhận xét: Nói chung, số điểm dữ liệu là quá ít để nhận thấy một mối liên hệ tuyến tính thực sự rõ ràng giữa các cặp biến phụ thuộc trong tất cả các kết hợp các nhóm của hai biến độc lập. Nhiều ô không thể vẽ được đường tuyến tính. Điều này sẽ được cải thiện rõ dệt khi tăng cỡ mẫu. Tạm thời chúng ta chấp nhận mối quan hệ tuyến tính giữa các cặp biến phụ thuộc trong tất cả các kết hợp các nhóm của hai biến độc lập.
b) Để kiểm tra giả định 9 rằng không có đa cộng tuyến giữa các biến phụ thuộc, bạn vui lòng đọc bài Phân tích tương quan Pearson. Kết quả phân tích tương quan Pearson cho ba biến Điểm Toán, Điểm Văn, Điểm Anh được thể hiện trong bảng dưới đây:
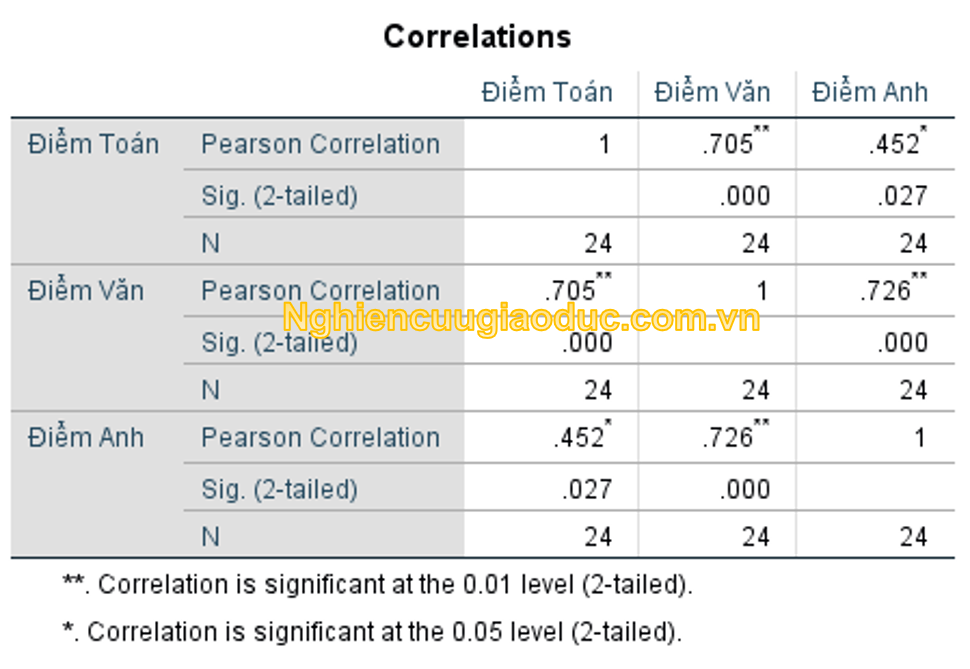
Nhận xét: Bảng phân tích tương quan Pearson cho điểm thi của học sinh cho thấy các biến Điểm Toán, Điểm Văn và Điểm Anh có mối tương quan là không lớn hơn 0.9 (nhiều sách thống kê cài đặt tương quan cao là 0.6 hoặc 0.8 trở lên) để dự báo một đa cộng tuyến. Nói chung, giả định về không có đa cộng tuyến là được chấp nhận.