Bài 4. Phân tích hiệp phương sai hai chiều (Two-way ANCOVA)
3. Kiểm tra ANCOVA hai chiều trong SPSS
Trở lại ví dụ 1, một nhà nghiên cứu muốn kiểm tra liệu thành tích thi Toán có khác nhau hay không dựa trên mức độ lo lắng trong bài kiểm tra giữa các sinh viên hay không. Họ cũng muốn hiểu cách các mức độ lo âu này được so sánh ở những thời gian ôn tập phân loại theo ‘ôn tập đều’ và ‘chỉ ôn tập khi sắp thi’. Các sinh viên có thời gian ôn tập khác nhau và nhà nghiên cứu muốn kiểm soát những khác biệt về lượng thời gian ôn tập này. Do đó, trong nghiên cứu này, hai biến độc lập là “mức độ lo lắng khi kiểm tra” (có ba nhóm – “0 = sinh viên lo âu thấp”, “1 = sinh viên lo âu trung bình” và “2 = sinh viên lo âu cao”), và “thời điểm ôn tập” (với hai loại, “0 = ôn tập đều” và “1 = chỉ ôn tập khi sắp thi”), biến phụ thuộc là “thành tích thi toán” (đo từ 0-100 điểm) và hiệp biến liên tục là “giờ ôn tập” (tức là tổng số giờ ôn tập toán). Các sinh viên đã được phát một bảng câu hỏi để xác định mức độ lo lắng khi làm bài kiểm tra của họ. Tiếp theo, điểm thi của các sinh viên đã được ghi lại. Cuối cùng, lượng thời gian mỗi sinh viên dành cho việc ôn tập đã được ghi lại.
Các nhà nghiên cứu muốn biết: (a) liệu các mức độ lo lắng ảnh hưởng như thế nào đến thành tích thi toán của các sinh viên; và (b) liệu thành tích thi toán theo các mức độ lo âu khi kiểm tra có khác nhau hay không tùy thuộc vào thời lượng ôn tập được phân loại trong ‘ôn tập đều’ và ‘chỉ ôn tập khi sắp thi’. Mức ý nghĩa Alpha được chọn là 5%.
3.1. Kiểm tra giả định
Trước khi thực hiện bài kiểm tra ANCOVA hai chiều, chúng ta cần tiến hành các bài kiểm tra một số giả định cơ bản. Một số giả định kiểm tra được giải thích trong kết quả của ANCOVA, trong khi dưới đây là các giả định phải kiểm tra độc lập.
3.1.1. Kiểm tra giả định 5 – hiệp biến phải có liên quan tuyến tính với biến phụ thuộc cho mỗi tổ hợp các nhóm của các biến độc lập.
– Bước 1: Nhấp vào Graphs > Legacy Dialogs > Scatter/Dot. Sau đó chọn Matrix Scatter và nhấp vào Define.
– Bước 2: Chuyển hiệp biến ‘Gioontap’ và biến phụ thuộc ‘Diemtoan’ vào ô Matrix Variables. Chuyển biến độc lập ‘Loau’ và ‘Cachontap’ vào ô Rows hoặc Columns.
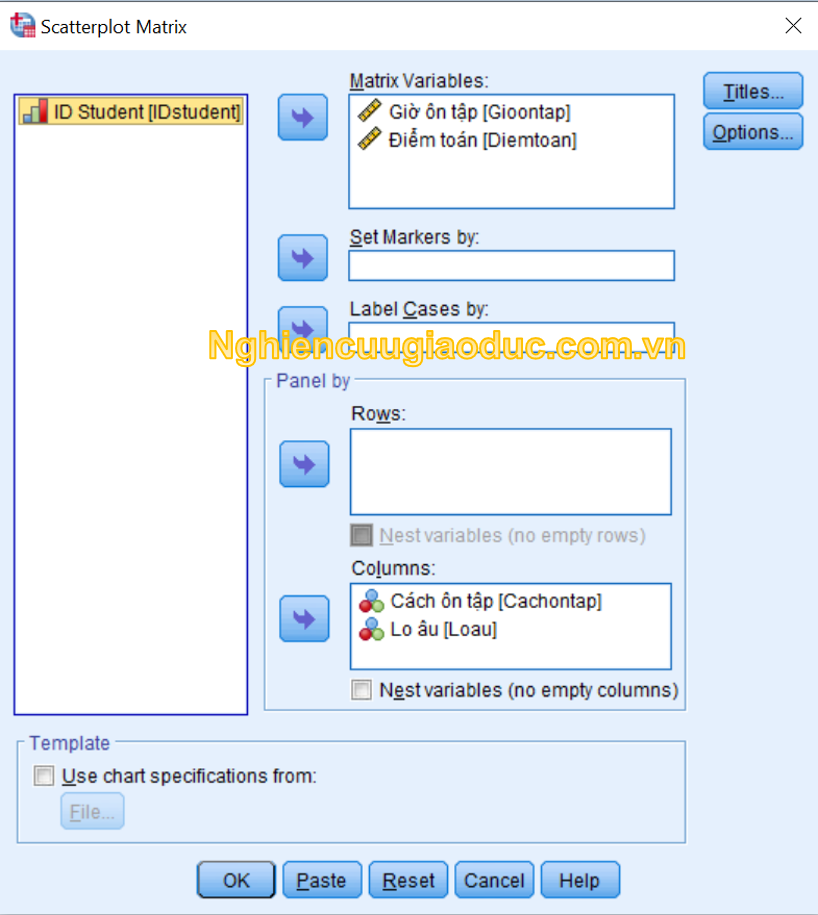
– Bước 3: Nhấp OK để chạy kết quả như hình dưới đây:
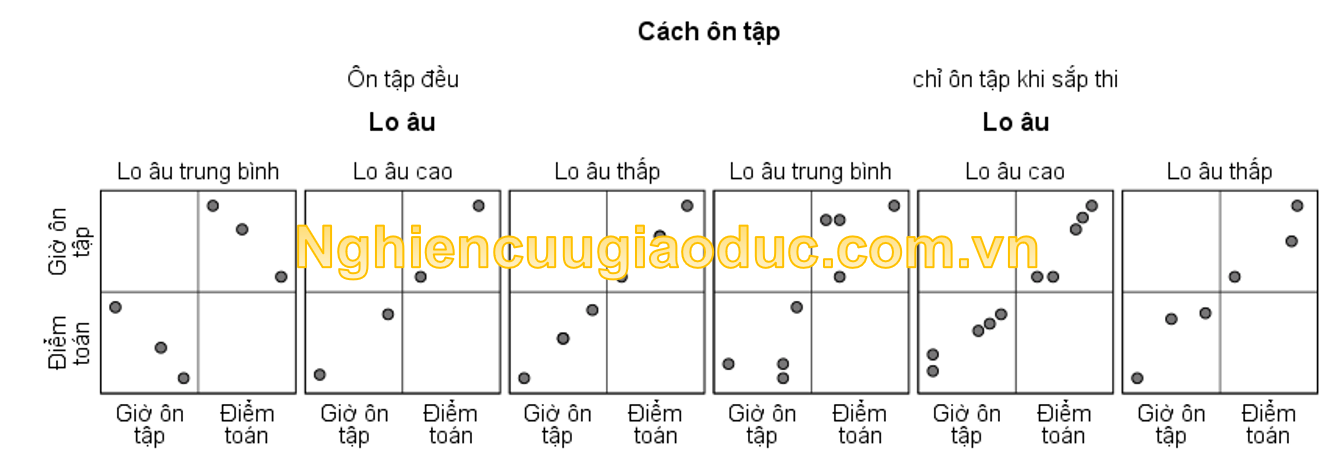
Nhận xét: Số điểm dữ liệu là ít, nhưng chúng ta vẫn cảm nhận nhận thấy một mối liên hệ tuyến tính giữa một hiệp biến ‘Gioontap’ và biến phụ thuộc ‘Diemtoan’. Điều này có thể được cải thiện khi tăng cỡ mẫu. Nhưng với tính chất minh họa (và có thể do số điểm dữ liệu quá ít), chúng ta tạm chấp nhận giả định số 5 được đáp ứng.
3.1.1. Kiểm tra giả định 6: Cần có sự đồng nhất của độ dốc hồi quy.
Giả định này kiểm tra rằng mối quan hệ giữa hiệp biến và biến phụ thuộc, được đánh giá bằng độ dốc hồi quy, là giống nhau trong mỗi ô của thiết kế (nghĩa là đối với mỗi tổ hợp nhóm của hai biến độc lập).
– Bước 1: Nhấp vào Analyze > General Linear Model > Univariate…
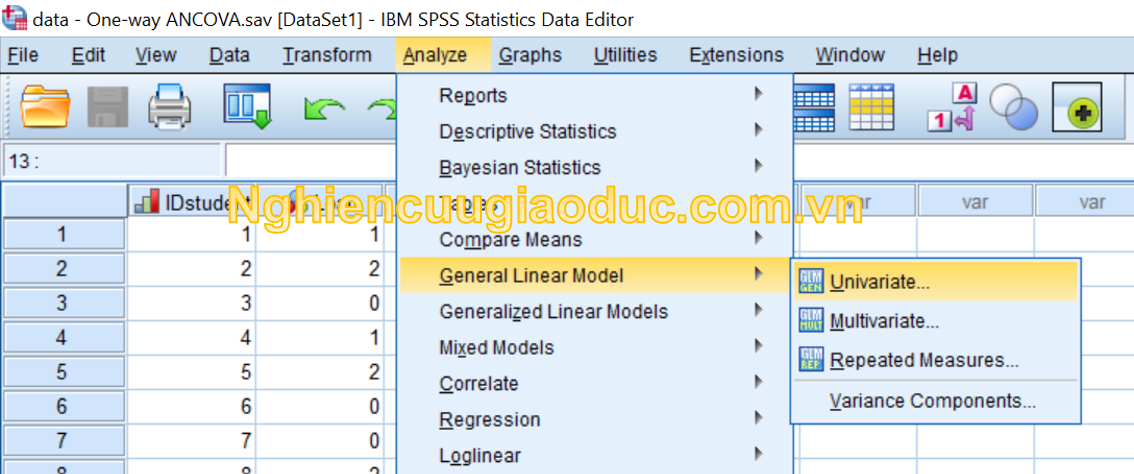
– Bước 2: Trong hội thoại Univariate, bạn chuyển biến phụ thuộc ‘Diemtoan’ vào ô Dependent Variables; chuyển biến độc lập ‘Loau’ và ‘Cachontap’ vào ô Fixed Factor(s); chuyển hiệp biến ‘Gioontap’ vào ô Covariate.
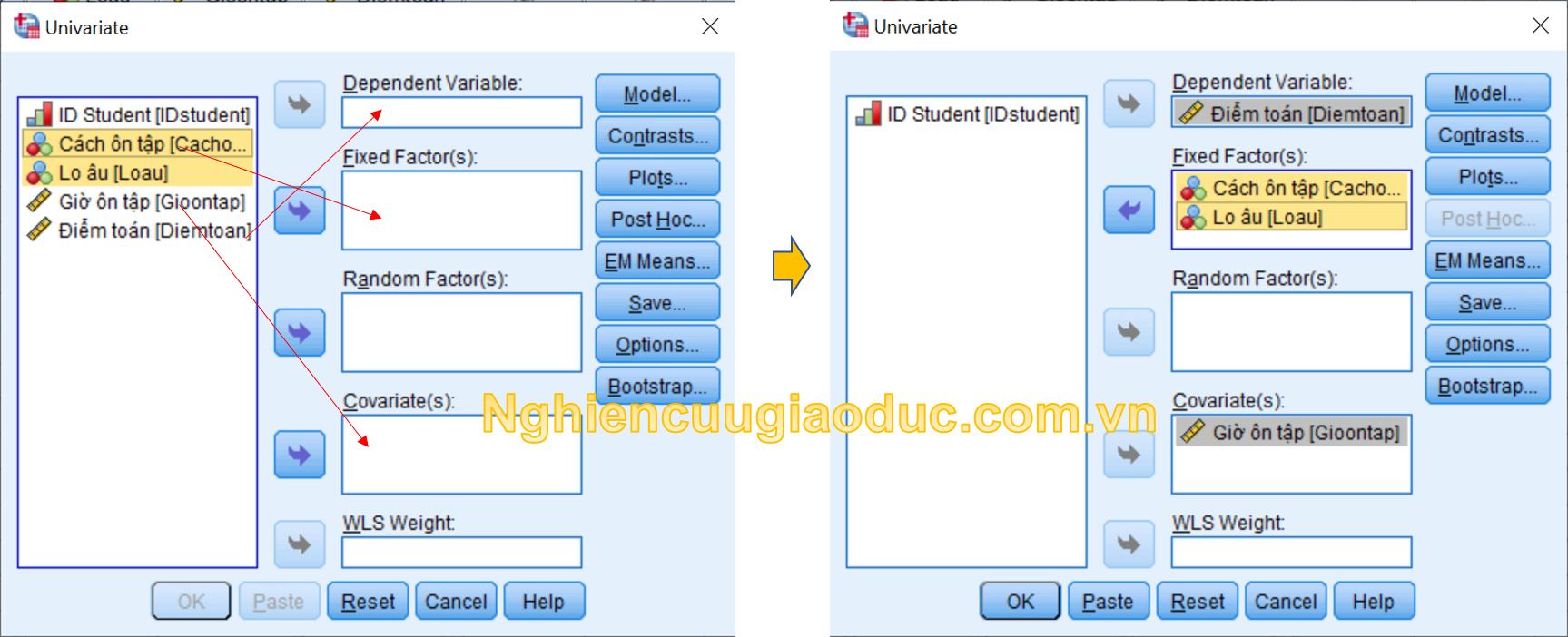
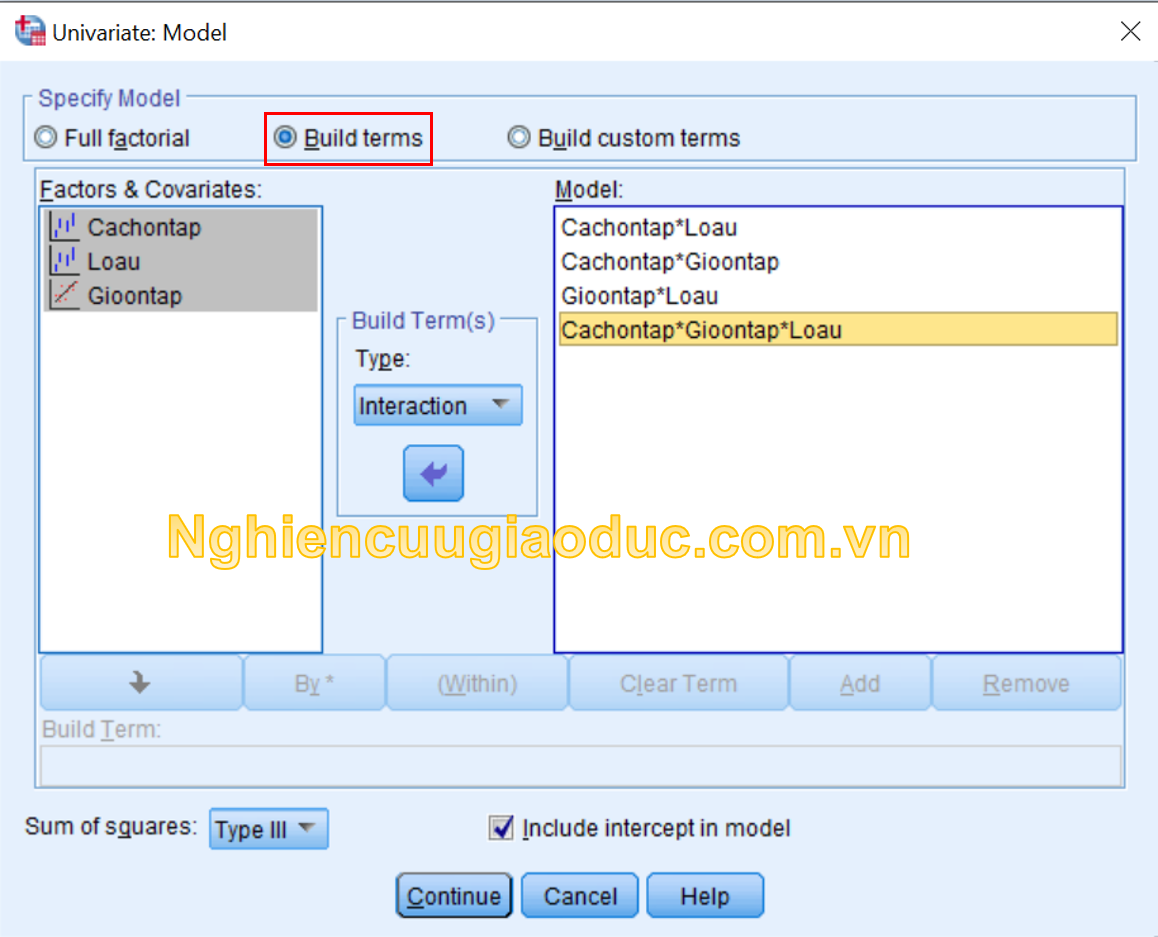
– Bước 3: Nhấp vào nút Model để mở hộp thoại Univariate: Model. Nhấp vào lựa chọn Build terms, sau đó chúng ta tạo ra các hiệu ứng tương tác gồm ‘Cachontap*Loau’, ‘Cachontap*Gioontap’, ‘Gioontap*Loau’, ‘Cachontap *Gioontap*Loau’ trong ô Model. Sau đó nhấp vào Continue.
– Bước 4: Nhấp OK để chạy kết quả.
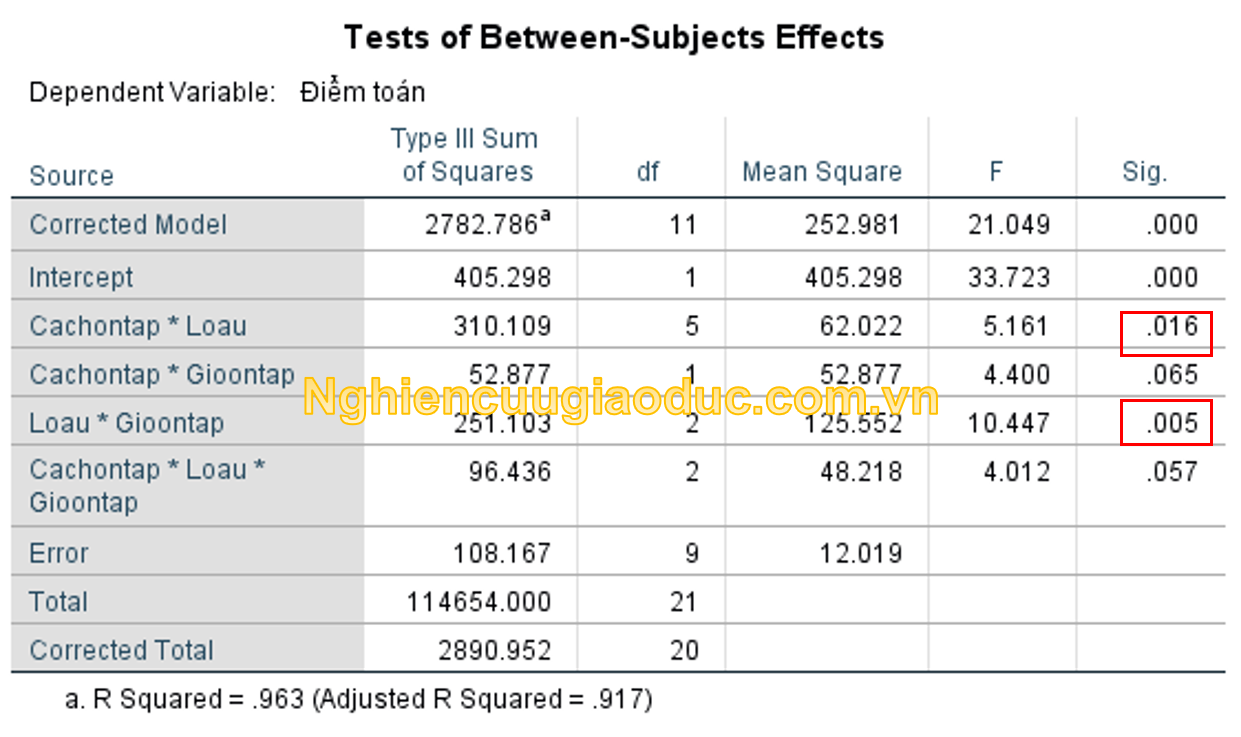
Kết quả trong bảng Test of Between-Subjects Effects, chúng ta kiểm tra giá trị tại hàng ‘Cachontap*Loau’, ‘Cachontap*Gioontap’, ‘Gioontap*Loau’, ‘Cachontap *Gioontap*Loau’ kết hợp cột ‘Sig.’ tức là các giá trị ‘p’. Kết quả cho thấy giá trị p-value tại các hàng ‘Cachontap*Loau’ và ‘Gioontap*Loau’ là có p < 0.05, tức là có ý nghĩa thống kê nên chúng ta bác bỏ giả thuyết vô hiệu, nghĩa là giả định về sự đồng nhất của độ dốc hồi quy là không được đáp ứng. Chúng ta không nên tiếp tục thực hiện phân tích ANCOVA hai chiều. Tuy nhiên, với tính chất minh họa thủ tục phân tích ANCOVA, chúng tôi vẫn tiếp tục thực hiện.
Các giả định khác được kiểm tra trong kết quả đầu ra của ANCOVA hai chiều.




















